Н. Воробьев
Все цифровые комбинационные узлы являются многофункциональными, то есть они могут выполнять функции,
специально для них не предусмотренные. В ряде случаев эти узлы обеспечивают некоторые схемные преимущества
перед специализированными, предназначенными для реализации этих функций. Мультиплексор является наиболее
характерным многофункциональным узлом.
1. Использование мультиплексора по прямому назначению [1]. В качестве примеров можно привести
следующие: мультиплексирование многоразрядного адреса микросхем памяти; мультиплексное управление
многоразрядными многоэлементными индикаторами [12]; последовательный опрос многих переменных, датчиков
и других однобитовых источников информации; временное уплотнение аналоговых сигналов в телефонии;
мультиплексирование выходных данных тестопригодных БИС; построение многоканальных коммутаторов, осциллографов.
2. Реализация произвольных функций алгебры логики на мультиплексорах.
Пусть требуется реализовать ФАЛ, зависящую от двух переменных и представленную таблицей истинности
(табл. 1). Запишем обобщенную форму СДНФ для этой функции и одновременно уравнение для MS 4╝1:
Yфал = x1x0 .1+x1x0 .0+x1x0.0+x1x0.1 (1)
YMS = a1a0.D0+a1a0.D1+a1a0.D2+a1a0.D3 (2)
Таблица 1
| N набора | х1 | х0 | y |
| 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 1 | 1 |
Очевидно полное совпадение выражений (1) и (2), из которых следует: если логические переменные
x1 и x0 подать на соответствующие адресные входы а1 и а0 MS 4╝1, то на его информационные входы
D0, D1, D2 и D3 нужно подать соответственно 1, 0, 0 и 1 (рис. 1).
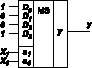
Рис. 1
В общем случае можно сформулировать следующее правило: если количество логических переменных n,
от которых зависит реализуемая ФАЛ, совпадает с разрядностью адресной части мультиплексора, то
эти переменные подаются на адресные входы мультиплексора (старшая переменная на старший адресный
вход), а на информационные входы мультиплексора MS 2n╝1 константы 0 и 1 в соответствии с таблицей
истинности реализуемой ФАЛ.
![]()
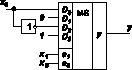
Рис.2 Рис.3
Реализуем на том же MS 4╝1 ФАЛ, зависящую от трех переменных (табл. 2). Запишем для нее
минимальную дизъюнктивную нормальную форму (МДНФ), воспользовавшись картой Карно, представленной на рис. 2.
Таблица 2
| N набора | x2 | x1 | x0 | y |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 0 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 1 |
y = x2x1x0+x2x0+x2x1 (3)
Преобразуем выражение (3) к виду, аналогичному выражению (1):
y = x2x1.x0+x2x1.0+x2x1 .x0+x2x1.1, (4)
где произведение x2x1.0 введено, чтобы в выражении (4) были представлены все четыре конституенты единицы двух
переменных x2 и x1. Сравнивая выражения (4) и (2), опять видим их полное соответствие. Отсюда вывод: на адресные
входы а1 и а0 MS 4╝1 нужно подать логические переменные x2 и x1, а информационные входы D0, D1, D2 и D3 для
произвольной ФАЛ, зависящей от трех переменных, в общем случае являются функциями от третьей переменной x0.
Такими функциями являются 0, 1, x0 и x0. Реализация данной ФАЛ представлена на рис. 3. Тот же результат проще
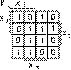
получить, если в табл. 2 выделить четыре группы по две строки в каждой и отделить переменную x0 от x2 и x1 (табл. 3).
Таблица 3
| N набора | x2 | x1 | x0 | y |
| 0 1 |
0 0 |
0 0 |
0 1 |
0 1 |
| 2 3 |
0 0 |
1 1 |
0 1 |
0 0 |
| 4 5 |
1 1 |
0 0 |
0 1 |
1 0 |
| 6 7 |
1 1 |
1 1 |
0 1 |
1 1 |
Видно, что переменные x2 и x1 образуют четыре набора, на каждом из которых функция y зависит только от одной
переменной x0, причем значения y = f(x0) легко выявляются из этой таблицы.
Для общего случая можно сформулировать следующее правило: если количество логических переменных n, от которых
зависит реализуемая ФАЛ, на единицу больше разрядности адресной части мультиплексора, то данную ФАЛ можно
реализовать на мультиплексоре MS 2n╝1 и одном инверторе.
Если распространить данный метод на реализацию ФАЛ, зависящую от четырех переменных, на том же MS 4╝1,
то очевидно, что если две старшие переменные x3 и x2 подать соответственно на адресные входы а1 и а0, то
информационные входы будут функциями двух младших переменных x1 и x0. Всего таких функций 16, из них
6 вырожденные (0, 1, x1, x0, x1, x0), а 10 функций зависят от двух переменных, причем для реализации
последних требуются 8 различных логических элементов (И, И-НЕ, ИЛИ, ИЛИ-НЕ, аb элемент запрета, а+b
элемент, реализующий функцию импликации, аb+аb элемент равнозначности и аb+аb элемент, реализующий
сумму по модулю два [2]. Итак, кроме мультиплексора, данная реализация потребует в худшем случае восемь
различных логических элементов, поэтому ее, как правило, не рекомендуется использовать.
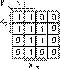
Рис. 4
В некоторых частных случаях ФАЛ, зависящую от четырех переменных, можно реализовать с использованием
только одного мультиплексора MS 4╝1 без каких либо логических элементов. Рассмотрим эти случаи. Пусть
требуется реализовать ФАЛ, представленную картой Карно (рис. 4). Если две старшие переменные x3 и x2
подать на адресные входы а1 и а0 MS 4╝1, то информационные входы D0, D1, D2 и D3 можно представить
четырьмя картами Карно для двух переменных x1 и x0 (рис. 5). Эти карты являются в данном случае строками
карты Карно, представленной на рис. 4. Из рис. 5 следует: D0 = x1x0, D1 = x0, D2 = x1+x0 и D3 = x1.
Соответствующая реализация показана на рис. 6.
Подадим теперь на адресные входы а1 и а0 соответственно переменные x1 и x0, тогда информационные входы
D0, D1, D2 и D3 можно представить четырьмя картами Карно для двух переменных x3 и x2 (рис. 7), причем
эти карты в данном случае столбцы карты Карно, данной на рис. 4. Из рис. 7 следует: D0 = 0, D1 = x2,
D2 = 1 и D3 = x3. Соответствующая реализация на рис. 8. Сравнивая рис. 6 и 8, делаем очевидный вывод
о предпочтительности реализации, представленной на рис. 8, так как здесь не требуется никаких логических элементов.
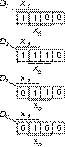
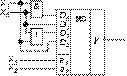
Рис. 5 Рис.6
Поиск рациональной структуры по данной методике в общем случае потребует анализа шести вариантов подачи
двух различных переменных из четырех на адресные входы MS 4╝1 (здесь шесть это число различных сочетаний
из четырех переменных по две). Проще рациональную структуру выявить, выполняя следующие процедуры:
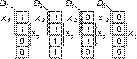
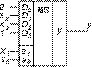
Рис.7 Рис.8
- Записать реализуемую ФАЛ в МДНФ. В нашем случае из рис. 4 следует:
y = x3x1+x1x0+x2x0 (5)
- Определить две переменные, наиболее часто встречающиеся в различных простых импликантах. В нашем случае это
x1 и x0, так как они встречаются по два раза, а переменные x3 и x2 только один. Именно переменные x1 и x0
необходимо подать на соответствующие адресные входы а1 и а0 MS 4╝1.
- Используя правило развертывания, законы дополнительности, одинарных элементов, поглощения и распределительный
закон первого рода [3], преобразовать МДНФ к виду, когда в выражении для реализуемой ФАЛ присутствуют все четыре
конституенты единицы двух переменных, выявленных в предыдущей процедуре. В нашем случае имеем:
y = x3x1+x1x0+x2x0 = x3x1.1+x1x0+x2.1.x0 =
x3x1(x0+x0)+x1x0+x2(x1+x1)x0 =
x3x1x0+x3x1x0+x1x0 +x2x1x0+x2x1x0 =
x2x1x0+x3x1x0+x1x0(1+x3+x2) =
x2x1x0+x3x1x0+x1x0 (6)
Представим теперь выражение (6) в виде, аналогичном выражению (1):
y = x1x0 .0+x1x0 .x2+x1x0 .x3+x1x0 .1 (7)
Сравнивая (7) и (2), выявляем: D0 = 0, D1 = x2, D2 = x3 и D3 = 1 (рис. 8). Эту методику можно распространить
и на реализацию систем двух или четырех ФАЛ с использованием 2- или 4-разрядных мультиплексоров, имеющих общую
адресную часть. Рациональный выбор переменных, подаваемых на адресные входы мультиплексоров, определяются подсчетом
общего числа каждой переменной, входящей в две или четыре функции, и в качестве адресных выбираются те, которые
встречаются наибольшее число раз во всех простых импликантах всех реализуемых ФАЛ.
![]()
Рис.9 Рис.10
Если использовать стробируемые MS 2n╝1, имеющие три состояния выхода, то любую ФАЛ, зависящую от n+2 переменных,
легко реализовать на двух стробируемых мультиплексорах и двух инверторах. Один из инверторов используется в цепи
стробирования одного из мультиплексоров, другой на их информационных входах. Рассмотрим пример. Пусть
ребуется реализовать ФАЛ, представленную картой Карно на рис. 9, на стробируемых мультиплексорах MS 4╝1,
имеющих три состояния выхода и активный уровень 0 на стробирующих входах. Представим эту карту в виде двух,
зависящих от трех младших переменных (рис. 10). Подавая переменную x3 непосредственно на стробирующий вход
одного из мультиплексоров MS 4╝1, мы реализуем функцию y1 (карта Карно, рис. 10а) и через дополнительный внешний
инвертор на вход другого y2 (рис. 10б). Очевидно, что y = y1+y2, причем логическая операция ИЛИ здесь монтажная
операция соединения в единую цепь выходов этих двух мультиплексоров. Подавая переменные x2 и x1 на соответствующие
адресные входы а1 и а0, а переменную x0 непосредственно или через второй дополнительный внешний инвертор вместе с
константами 0 и 1 на информационные входы мультиплексоров, получаем окончательную реализацию ФАЛ (рис. 11).
Отметим, что функции y1 и y2 можно реализовать по рациональным структурам, способы получения которых описаны выше,
так как на адресные входы двух мультиплексоров не обязательно подавать одни и те же переменные.
Реализацию одной ФАЛ на мультиплексоре можно рассматривать как одноразрядное ПЗУ, а систем n ФАЛ, зависящих от
одних и тех же переменных как n-разрядное ПЗУ.
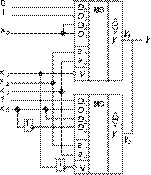
Рис. 11
3. Мультиплексор в режиме сдвигателя. Сдвигателем называется цифровой комбинационный узел, предназначенный для
сдвига n-разрядного слова на любое число разрядов в диапазоне от 0 до m за один такт. Имеется в виду, что смена
однопозиционного управляющего сигнала вызывает немедленное (через время, определяемое задержками распространения
сигналов через логические элементы) выполнение требуемой микрооперации. Рассмотрим уравнения для сдвигателя с
параметрами n = 4, m = 3 (разрядность входного слова X n = 4, разрядность выходного слова Y n+m = 7, сдвиг может
быть реализован на 0, 1, 2 и максимум на три разряда).
y0 = S0x0
y1 = S0x1+S1x0
y2 = S0x2+S1x1+S2x0
y3 = S0x3+S1x2+S2x1+S3x0 (8)
y4 = S1x3+S2x2+S3x1
y5 = S2x3+S3x2
y6 = S3x3,
где S0 однопозиционный управляющий сигнал; при его активном состоянии S0 = 1 и S1 = S2 = S3 = 0 обеспечивается
передача входного слова на выход без сдвига, при S1 = 1 и S0 = S2 = S3 = 0 осуществляется сдвиг входного слова на
один разряд и т. д.
Для реализации этих уравнений требуются двухвходовые элементы И и элементы ИЛИ на 2, 3 и 4 входа.
Так как в данном случае выполняется четыре микрооперации (m = 0, 1, 2 или 3), то наиболее просто реализовать такой
сдвигатель на семи одноразрядных MS 4╝1, используя их адресные входы как управляющий код числа m (табл. 4).
Таблица 4
| N набора | а1 | а0 | m |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 2 | 1 | 0 | 2 |
| 3 | 1 | 1 | 3 |
Схема такого сдвигателя приведена на рис. 12. На свободные входы мультиплексоров подаются сигналы, характер
которых определяется конкретным алгоритмом, реализуемым операционным узлом (логический, арифметический,
циклический сдвиг и т. п.)
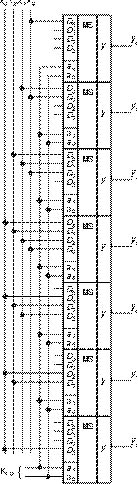
Рис. 12
4. Мультиплексор преобразователь параллельного кода в последовательный. Схема такого преобразователя
приведена на рис. 13. Здесь четырехразрядный параллельный код с выходов регистра подается на информационные
входы MS 4╝1, адресные входы которого подключены к выходам 2-разрядного счетчика. Если счетчик изменяет
свои состояния от тактовых импульсов в последовательности 0, 1, 2, 3, то на выходе мультиплексора появляются
разряды слова, начиная с младшего; если как 3, 2, 1, 0, то начиная со старшего. Варианты схем, использующих
эту структуру, чрезвычайно разнообразны.
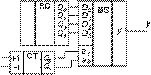
Рис. 13
5. Мультиплексор в составе многоканального селектора. Многоканальным селектором называется цифровой
комбинационный узел, имеющий n входов и m выходов, с возможностью передачи данных с любого входа в любой
выход при использовании между входами и выходами минимального числа линий связи. Рассмотрим конкретную
схему для случая n = m = 8. Общая идея: из 8 входов передадим данные в одну линию с помощью мультиплексора,
а затем из этой линии передадим данные на 8 выходов с помощью однобитового селектора. Схема приведена на
рис. 14, где обозначено: src (source) источник, dst (destination) приемник, А адрес источника,
В адрес приемника. В качестве однобитового селектора используется двоично-десятичный дешифратор с
активным нулем на выходах. При А = В реализуется алгоритм передачи данных scri ╝ dsti, а при
А = В scri ╝ dstj, i = 0...7, j = 0...7.
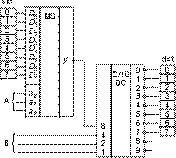
Рис. 14
6. Мультиплексор в составе компаратора двух чисел, вырабатывающего осведомительный сигнал А = В. Если в
распоряжении разработчика нет специализированного компаратора, то его можно реализовать, используя совместно
дешифратор и мультиплексор. Определение, структура и применение специализированного компаратора будут
рассмотрены в следующей статье учебного цикла. На рис. 15 приведена схема компаратора, сравнивающего два
3-разрядных числа. В ней используются дешифратор "1 из 8" с активной единицей выхода и мультиплексор
MS8╝1 с прямым выходом. При А = В активная единица с выхода дешифратора передается на выход мультиплексора и,
следовательно, Fa=b= 1. При А = В на выход будет передаваться сигнал 0 (Fa=b= 0). Рекомендуется самостоятельно
реализовать компаратор двух 2-разрядных чисел, используя один MS 8╝1 и один инвертор (см. раздел 2 данной статьи).
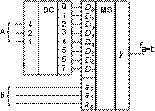
Рис. 15
7. Мультиплексор в составе контроллера состояния сложного объекта. Постановка задачи: пусть сложный цифровой
блок разбит на 8 функционально законченных узлов источник вторичного питания, операционный блок, память,
система синхронизации, устройство управления и т. д. Каждый из этих узлов снабжен встроенной системой контроля
работоспособности. Если узел исправен, то система контроля выставляет осведомительный сигнал 1, если нет 0.
Требуется быстро определить неработоспособный узел и заменить его. Схема контроллера, выполняющего поставленную
задачу, приведена на рис. 16, где обозначено: G генератор тактовых импульсов, СТ трехразрядный суммирующий
счетчик, DC дешифратор "1 из 8", в качестве дисплея используется один 7-сегментный индикатор.
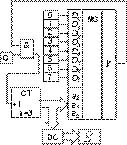
Рис. 16
Если все функциональные узлы 0...7 в порядке, то независимо от адреса мультиплексора y = 1, вентиль И открыт,
счетчик циклически изменяет свои состояния, дешифратор их дешифрирует и при частоте генератора более 200 Гц
на индикаторе светится с половинной яркостью символ 8, указывающий на полную работоспособность цифрового блока.
Пусть в какой-то момент времени узел с номером 6 обнаружил, что он неисправен, и на нем выставляется осведомительный сигнал 0.
Как только счетчик примет состояние 6, на выходе мультиплексора появится сигнал 0, который запрет вентиль И. Счетчик
останется в том же состоянии, а на 7-сегментном индикаторе высветится 6. После замены узла 6 на индикаторе снова появится символ 8.
8. Мультиплексор MS 2-1 в качестве тактируемого потенциалом D-триггера.Уравнение MS2-1 имеет вид:
y = a0D0 + a0D1 (9)
Характеристическое уравнение тактируемого потенциалом D-триггера с активной единицей на тактовом входе имеет вид:
Qt+1 = Ct+1Qt + Ct+1Dt, (10)
и с активным нулем на тактовом входе:
Qt+1 = Ct+1Dt + Ct+1Qt (11)
где индекс t соответствует текущему состоянию сигналов (до переключения), а t+1 следующему после переключения.
Полагая в уравнении (9) y = Qt+1, D0 = Qt, D1 = Dt и a0 = Ct+1, получаем выражение Qt+1 = Ct+1Qt + Ct+1Dt, полностью
совпадающее с уравнением (10).
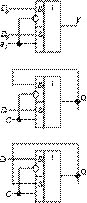
Рис. 17
Полагая в уравнении (9) y = Qt+1, D0 = Dt, D1 = Qt и a0 = Ct+1, получаем выражение Qt+1 = Ct+1Dt + Ct+1Qt, полностью
совпадающее с (11). Итак, на одном и том же MS 2╝1 можно получить схему потенциально управляемого D-триггера с
активными нулем или единицей на тактовом входе. Схема MS 2╝1 и соответствующие D-триггеры приведены на рис. 17.
9. Мультиплексоры MS 2╝1 в качестве сдвигового регистра. Полученные выше D-триггеры являются прозрачными. Этот
термин говорит о том, что при активном сигнале на тактовом входе изменения данных на D-входе немедленно передаются
на выход. Известно, что на прозрачных D-триггерах с одним и тем же активным сигналом на тактовых входах нельзя
построить сдвиговый регистр. Однако, чередуя триггеры с различными активными сигналами на тактовых входах, это
возможно, причем сдвиг данных в нем будет осуществляться как фронтом (переходом 01), так и спадом (переходом 10)
на тактовом входе [4]. Хорошим примером может служить схема (рис. 18а) регистра, построенная на интегральной
схеме счетверенного мультиплексора типа КР1533КП16 (SN74ALS157A), где DR (data right данные справа)
последовательный вход в младший разряд при сдвиге в сторону старших разрядов. На рис. 18б приведена временная
диаграмма работы данного сдвигового регистра.
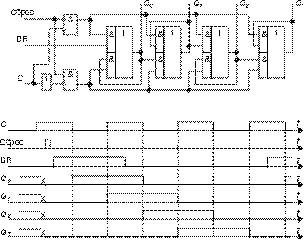
Рис. 18
Примечания к рис. 18а:
- C = 0 - активный уровень для разрядов Q0 и Q2, C=1 - для Q1 и Q3.
- Так как отдельно работающие триггеры прозрачны, необходимо помнить: во-первых, обнуление регистра надо осуществлять при С=1, в противном случае при С=0 после снятия сигнала "сброс" (активная единица) разряд Q0 немедленно примет значение сигнала DR; во-вторых, данные на последовательном входе DR надо менять при С=0 (неактивном сигнале для разряда Q0).
- Как видно из временных диаграмм, данные сдвигаются таким регистром с перекрытием.
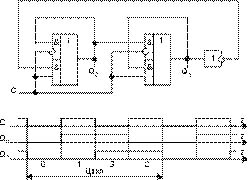
Рис. 19
10. Мультиплексоры в режиме кольцевого счетчика. Кольцевым счетчиком называется сдвиговый регистр, замкнутый
в кольцо. Рассмотрим кольцевой 2-разрядный счетчик с одной перекрестной связью (такие структуры называются
счетчиками Джонсона). Его схема приведена на рис 19а, а временные диаграммы работы на рис. 19б. Как видно из
временных диаграмм, счетчик имеет четыре состояния в течение двух тактов синхронизации.
Если рассматривать только один выход Q1, то данную схему можно считать счетным триггером, срабатывающим по
переходу 10 на входе С, а если только один выход Q0, то ее же можно считать счетным триггером, срабатывающим
по переходу 01.
Ограничившись рассмотренными выше простыми схемами применения мультиплексора, перечислим более сложные варианты
использования, опубликованные в литературе. В работе [1] рассмотрена структура и возможные режимы работы
универсального селектора мультиплексора типа К561КП2, способного обрабатывать не только цифровые, но и
аналоговые сигналы. В [5] показан способ уменьшения емкости памяти с помощью входного мультиплексора. В [6]
предложена мажоритарная схема с приоритетом. В [7] рассмотрена схема двоичного шифратора клавиатуры,
нечувствительного к "дребезгу" контактов. В [8] предлагается использование мультиплексора для повышения
производительности микропроцессора за счет рациональной обработки сигналов запроса на прерывание. В [9] описаны
типичные варианты применения программируемого мультиплексора: управление прохождением информации, расшифровка
команд микропрограммируемой машины, реализация цифрового хронирующего генератора. В [10] рассматриваются
"статистические" или "разумные" мультиплексоры, дающие возможность реализовать в сетях передачи данных многие
функции, свойственные более дорогим сетевым процессорам с микропрограммным управлением и концентратором.
Другое достоинство статистических мультиплексоров в том, что их распределенная логика позволяет им также
работать в качестве модемов и устройств коммутации. В [11] описывается структура цифрового логарифмического
преобразователя, который сжимает 8-разрядный двоичный код в 5-разрядный в соответствии с законом 2n╝ 4n. В [12]
подробно рассматривается эффективная адресация жидкокристаллических индикаторов.
Литература


 Мультиплексор как многофункциональный узел
Мультиплексор как многофункциональный узел