PDFs

Новости

Литература

Схемы

Форум

Блоги

Реклама

Читать @chipinforu
Мне нравится

В. Голуб

Взгляд на сигма-дельта АЦП

    Существует класс АЦП, использующих сигма-дельта (SD) преобразование , обладающее рядом преимуществ. Сигма-дельта АЦП выпускаются многими фирмами, среди которых ведущее место занимает Analog Devices, давшая их описание в [13]. Сигма-дельта АЦП описаны также в [4,5], что способствует их пониманию и популяризации. Ниже приводятся результаты анализа сигма-дельта АЦП, дополняющие работы [15].
    Сигма-дельта АЦП содержит (рис. 1а):

• сигма-дельта модулятор "u -> f ";
  
• преобразователь сигнала сигма-дельта модулятора в цифровой сигнал "f -> код";
  
• цифровой фильтр-дециматор "ЦФД".
  
  

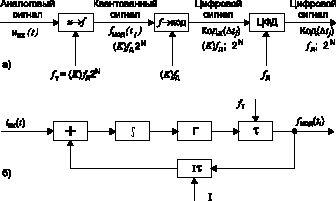
Рис. 1

    В современных сигма-дельта АЦП преобразование осуществляется с избыточной дискретизацией (передискретизацией), цифровой фильтрацией и децимацией преобразуемого сигнала. Практическая схема сигма-дельта АЦП без дополнительных преобразований дана в [6].
    Сигма-дельта модулятор и квантование частоты. Сигма-дельта модулятор является преобразователем аналогового сигнала в частотно-модулированную последовательность отсчетов, синхронизированную тактовыми импульсами. Основой сигма-дельта модулятора является ЧИМ модулятор с непрерывным интегрированием и уравновешиванием заряда по схеме на рис. 1б, но без цепи тактовых импульсов "f_т". ЧИМ модулятор содержит: "+" сумматор, "т" интегратор, "й" компаратор, "t" формирователь прямоугольных импульсов напряжения с нормированной длительностью и "I_t" формирователь прямоугольных импульсов тока с нормированным током и результирующей площадью S_I = I_t = const. Компаратор и, соответственно, формирователи импульсов ЧИМ модулятора, в отличие от рассмотренного ниже сигма-дельта модулятора, срабатывают при достижении напряжением интегратора уровня компарирования.
    Частота следования импульсов ЧИМ модулятора

f_мод(t_i) = K_модi_вх(t_i) = [i_вх(t_i)/I ]/t,

где K_мод = 1/S_I коэффициент преобразования, а f_мод(t_i) и i_вх(t_i) мгновенные значения частоты и тока в дискретных точках t_i, определяемых временным положением импульсов модулятора [7]. В статическом режиме, при i_вх(t) = i_вх = const,

f_мод(t_i) = f_мод = K_модi_вх = (i_вх/I )/t.      (1)

    На рис. 2а показаны последовательности импульсов на выходе ЧИМ модулятора. Слева на рисунке записаны частоты следования импульсов f_мод = (1/3)/t, ... (2/3)/t, пропорциональные постоянным значениям тока i_вх= I/3, ... 2I/3.
    Обычно входной величиной модулятора является напряжение u_вх(t) = i_вх(t)R, где R сопротивление резистора на входе интегратора. Кроме того, на вход модулятора вместе с сигналом подается напряжение смещения, обеспечивающее входному току направление, противоположное направлению тока I формирователя импульсов, и "привязку" нулевого уровня сигнала к середине (или другому значению) частотной шкалы на выходе модулятора. Соответственно, i_вх(t) = i_с(t) + I_см или, в статическом режиме, i_вх = i_с + I_см, где i_с(t) и i_с ток сигнала, а I_см ток смещения.

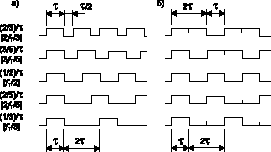
Рис. 2

    Сигма-дельта модулятор это синхронизированный ЧИМ модулятор по схеме на рис. 1б с цепью "f_т". На рис. 2б показаны последовательности импульсов сигма-дельта модулятора, причем с теми же частотами следования, что и для ЧИМ модулятора (рис. 2а). Последовательности импульсов сигма-дельта модулятора, в отличие от ЧИМ модулятора, характеризуются следующим:

• длительности импульсов и интервалов кратны величине t = 1/f_т, где f_т частота следования тактовых импульсов, являющаяся частотой квантования по-следовательности импульсов. Частоты следования импульсов сигма-дельта модулятора, выраженные через f_т, записаны слева на рис. 2 в квадратных скобках;
  
• при частотах, больших f_т/2, эквивалентное увеличение частоты происходит не за счет уменьшения длительности интервалов, как на рис. 2а, а за счет увеличения длительности импульсов (рис. 2б). При этом, например, импульс с длительностью 2t при последующем цифровом преобразовании воспринимается как два импульса;
  
• последовательности импульсов с частотами следования
  ... f_т/5, f_т/4, f_т/3, f_т/2, 2f_т/3, 3f_т/4, 4f_т/5, ...
  состоят из одинаковых периодов (с неизменными в течение всей последовательности длительностями импульсов и интервалов). Последовательности с частотами f_т/3, f_т/2 и 2f_т/3 показаны на рис. 2б. Каждый период указанных последовательностей характеризуется тем же значением частоты, что и последовательности в целом. Назовем их квантованными частотами и обозначим f_мод.кв;
  
• последовательности с другими частотами следования импульсов характерны тем, что состоят из периодов с разными f_мод.кв. Примером являются показанные на рис. 2б последовательности с частотами 2f_т/5 и 3f_т/5, состоящие из чередующихся периодов с f_мод.кв, равными f_т/3, f_т/2 и f_т/2, 2f_т/3 соответственно. Частоты 2f_т/5 и 3f_т/5 являются средними частотами следования импульсов на интервале двух периодов (в общем случае, средние частоты могут быть определены на любом интервале D_tj, равном целому или нецелому числу нескольких периодов). Обозначим средние частоты как f_мод.ср(D_tj), для краткости f_мод.ср. При рассмотренном ниже преобразовании D_tj интервал дискретизации. Средняя частота пропорциональна преобразуемому сигналу (с возможной погрешностью, обусловленной тем, что интервал дискретизации конечен). Указанные выше частоты f_мод.ср = 2f_т/5 и 3f_т/5 пропорциональны i_вх = 2I/5 и 3I/5;
  
• чередование периодов с разными частотами обусловливает частотную манипуляцию, проявляющуюся в качестве шума квантования. Благодаря шумовой манипуляции обеспечивается пропорциональность зависимости средней частоты от входного сигнала.
  

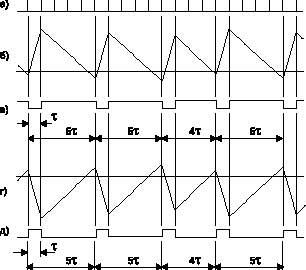
Рис. 3

    Процесс формирования последовательностей импульсов сигма-дельта модулятора показан на рис. 3, где а тактовые импульсы; б, в напряжение интегратора и выходная последовательность импульсов при i_вх = (11/14)I > I/2; г, д напряжение интегратора и выходная последовательность импульсов при i_вх = (3/14)I < I/2. На рис. 3б,г показаны также уровни компарирования. В отличие от ЧИМ модулятора, формирователи импульсов сигма-дельта модулятора срабатывают после срабатывания компаратора при поступлении очередного тактового импульса. На рис. 3г,д первые два периода напряжения интегратора равны 5t. В связи с задержкой срабатывания формирователей, сопровождаемой непрерывным интегрированием, в интеграторе накапливается избыточный заряд. В результате, очередное срабатывание формирователей происходит на один тактовый импульс раньше, и соответствующий этому срабатыванию период напряжения равен 4t (рис. 3г,д). Среднее значение частоты следования импульсов на интервале трех периодов равно fмод.ср = (3/14)/t = 3fт/14 и пропорцио-нально току iвх = (3/14)I. Режим работы сигма-дельта модулятора с i_вх > I/2 (рис. 3б,в) отличается от режима с i_вх < I/2. При токе i_вх > I/2 заряд в интеграторе возрастает настолько, что последующий разряд не успевает произойти в течение времени, равном t, и сбросить компаратор в исходное состояние. Сброс компаратора произойдет через больший промежуток времени, в результате чего длительность импульса, формируемого в течение времени разряда, будет равна 2t, 3t, ... . На рис. 3б,в показаны напряжение интегратора и последовательность импульсов модулятора при i_вх = (11/14)I и, соответственно, при средней частоте f_мод.ср = (11/14)/t = 11f_т/14.
    На рис. 4а показаны графики средней частоты f_мод.ср (прямая линия) и квантованных частот f_мод.кв (ступенчатые линии) в зависимости от тока i_вх. При i_вх = ... I/3, I/2, 2I/3, ... средние частоты равны квантованным, и "ошибка" квантования, соответственно, равна нулю. При других значениях i_вх возникает "ошибка" квантования, при которой каждому значению f_мод.ср, согласно рассмотренному на рис. 3, соответствуют квантованные значения частоты, чередующиеся в таком соотношении, при котором f_мод.ср определяется выражением (1). Например, рассмотренные выше на рис. 2б и показанные также на рис. 4а средние частоты 2f_т/5 и 3f_т/5 определяются квантованными частотами f_т /3, f_т/2 и f_т/2, 2f_т/3 соответственно. При этом "ошибку" квантования можно характеризовать положительной Df_шум+, отрицательной Df_шум- и суммарной Df_шум (Df_шум+ Df_шум-) амплитудами шума квантования.

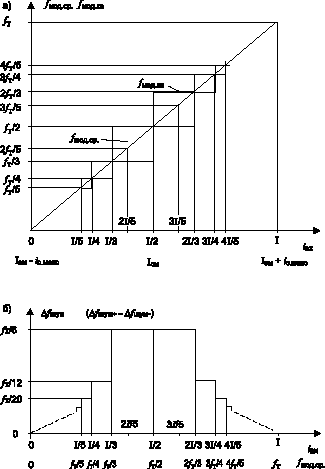
Рис. 4

    На рис. 4б показан график Df_шум в зависимости от f_мод.ср (на горизонтальной оси отложены также значения i_вх, которым соответствуют значения частот согласно рис. 4а). Диапазон частот модулятора (частот следования его импульсов) от 0 до f_т, а с учетом последующего цифрового преобразования до f_т(2N1)/2N. Максимальная амплитуда шума Df_шум = f_т/6 в диапазоне частот от f_т/3 до 2f_т/3, причем максимальная частота шумовой манипуляции равна F_шум = f_т/5 на средних частотах модулятора f_мод.ср = 2f_т/5 и 3f_т/5 (при Df_шум+ = f_т/10 и f_т/15, Dfшум- = -f_т/15 и -f_т/10, соответственно). При f_мод.ср ~ f_мод.кв = f_т/2, а также при f_мод.ср ~ f_мод.кв = f_т/3 и f_мод.ср ~ f_мод.кв = 2f_т/3 (в пределах от f_т/3 до 2f_т /3), суммарная амплитуда шума также равна Df_шум = f_т/6, но при Df_шум+ ~ Df_шум и Df_шум- ~ 0 (если f_мод.ср > f_мод.кв) и при Df_шум- ~ -Df_шум и Df_шум+ ~ 0 (если f_мод.ср < f_мод.кв), причем при частоте шумовой манипуляции F_шум -> 0 (одиночные "выбросы" частоты).
    Дискретизация и цифровой сигнал. Обычно в АЦП квантованию предшествует дискретизация преобразуемого сигнала. Отсчеты берутся в точках дискретизации и являются, соответственно, его мгновенными значениями. В сигма-дельта АЦП последовательность действий изменена. В сигма-дельта модуляторе осуществляется квантование (передискретизация) сигнала с частотой f_т, а затем, при цифровом преобразовании, "оформляется" его дискретизация с частотой f_д = f_т/2N, где N разрядность преобразования. Существенным является то, что отсчеты берутся не в точках дискретизации, а определяются средними значениями частоты следования импульсов на интервалах дискретизации Dt_j = 1/f_д. Последнее определяет частотную характеристику преобразования, функция которой

a(F/f_д) = sin(2pF/f_д)/(2pF/f_д),    (2)

где F частота модуляции, она же частота преобразуемого сигнала. Согласно (2), на частотах F = 0, f_д/8, f_д/4, f_д/2, где f_д/2 предельная частота согласно теореме Котельникова, a(F/f_д) = 1, 0,9, 0,64, 0, т. е. наблюдается плавный спад характеристики до нуля, требующий использования более узкого диапазона частот преобразуемого сигнала.
    Для возможности использования диапазона частот до f_д/2 может быть применена дополнительная передискретизация с частотой Kf_д, при соответственно увеличенной в K раз частоте квантования (на рис. 1а коэффициент K показан в скобках). При этом в (2) вместо f_д следует использовать Kf_д. Диапазон частот расширяется в K раз, в результате чего частотам до f_д /2 будет соответствовать почти равномерный участок частотной характеристики. Степень равномерности будет зависеть от величины K. После преобразования избыточное расширение частотного диапазона ограничивается выходным цифровым фильтром с децимацией отсчетов (рис. 1а).
    В [6] рассмотрен цифровой преобразователь, содержащий N-разрядный счетчик с регистром памяти и делитель частоты тактовых импульсов. Делитель предназначен для получения импульсов дискретизации. Отсчеты импульсов сигма-дельта модулятора, определяемые их совпадением с тактовыми импульсами, подаются на вход счетчика. Импульсы дискретизации управляют работой счетчика и регистра. Разрядные выходы регистра являются выходом цифрового сигнала в параллельном коде.

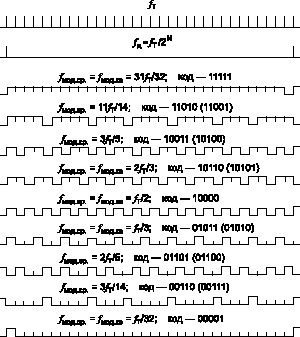
Рис. 5

    На рис. 5, наряду с тактовыми импульсами (fт), показаны импульсы дискретизации (fд), а также сделана разметка интервалов дискретизации с заполнением их импульсами сигма- дельта модулятора. На каждом интервале дискретизации отсчеты импульсов модулятора, подсчитываемые счетчиком, определяют текущий код цифрового сигнала. Значения кодов записаны на рис. 5 рядом со значениями частот следования импульсов (отсчетов). При работе счетчика в соответствии с (2) осуществляется фильтрация сигнала, при которой подавляются шум квантования, а также высокочастотный шум входного сигнала. Указанную фильтрацию можно объяснить также тем, что результат подсчета импульсов, определяемый их количеством на интервале дискретизации, не зависит от их шумовой частотной манипуляции в пределах интервала. На рис. 5 разрядность показана равной N = 5 (обычно N = 12 и более). Из рисунка следует, что количество импульсов на соседних интервалах будет разным, если частота следования импульсов не кратна частоте дискретизации (отличающийся код соседних интервалов показан в скобках). В этом случае в цифровом коде будет наблюдаться "мерцание" младших разрядов. Среднее значение мерцающих кодов пропорционально преобразуемому аналоговому сигналу. Влияние мерцания на конечный результат может быть снижено увеличением разрядности преобразования.

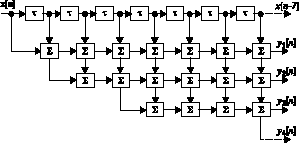
Рис. 6

    В работах [15] для цифрового преобразования сигнала сигма-дельта модулятора показано применение цифрового фильтра. На рис. 6 приведена возможная схема такого преобразования, где "t" элементы временной задержки, "S" комбинационные полусумматоры, x[n] входной и y1[n], y2[n], y3[n] трехразрядный выходной сигналы. Частота отсчетов может быть равной fт (или Kfт), но это избыточно, и она децимируется до fд. Разрядность преобразования может быть увеличена "наращиванием" схемы с использованием дополнительных выводов x[n-7] и y4[n]. В рассматриваемом преобразователе обеспечивается фильтрация в соответствии с (2). В [1] упоминается фильтр с кубической характеристикой (sina/a)3, обеспечивающей более качественную фильтрацию по сравнению с характеристикой (2) типа sina/a.
    Модуляторы высоких порядков. Рассмотренный выше сигма-дельта модулятор является модулятором 1-го порядка. Для повышения точности преобразования в сигма-дельта АЦП используются модуляторы высоких порядков, обладающие повышенным уровнем шума квантования в области частот за пределами полезного спектра сигнала и, соответственно, пониженным уровнем шума в области спектра [15]. Однако следует учитывать, что модуляторы высоких порядков обладают неравномерной частотной характеристикой, зависимой от постоянных времени интеграторов, входящих в состав модуляторов.
    Сигма-дельта модуляторы 2-го и n-го порядков описываются дифференциальными уравнениями

t₁f_мод▒(t) + f_мод(t) = K_модi_вх(t);

(t_n-1...t₁)f_мод(n-1)(t) + ... + tn-1f_мод▒(t) + f_мод(t) = K_модi_вх (t),

    где fмод(t) непрерывная функция частоты, представляемая как результат интерполяции дискретных значений fмод.ср(Dtj), а tn-1, ... t1 постоянные времени дополнительных интеграторов, включенных в модуляторе в перечисленной последовательности номеров, (tn-1...t1) их произведение.
    Приведенные уравнения аналогичны дифференциальным уравнениям полиномиальных ФНЧ, в связи с чем в данном вопросе к модуляторам применима теория указанных фильтров. Так, например, модуляторы 3- го порядка, описываемые функцией фильтрации 2-го порядка, характеризуются собственной частотой w0 = 1/Ц(t1t2) и добротностью Q = Ц(t1/t2). При Q = 1/Ц3 и 1/Ц2 реализуются, например, аппроксимации по Бесселю и Баттерворту. Частотные искажения, вносимые указанной фильтрацией, могут быть сведены к минимуму выбором соответствующих w0 и Q.
    Выводы. Сигнал сигма-дельта модулятора это квантованный частотно- модулированный сигнал с шумом квантования, усредняющим частоту модуляции (манипуляции) для обеспечения ее пропорциональной зависимости от входного аналогового сигнала. Точность усреднения тем выше, чем выше разрядность преобразования. Диапазон частот модулятора от 0 до fт(2N1)/2N. Максимальная амплитуда шумовой манипуляции, равная fт/6, в средней области диапазона частот модулятора от fт/3 до 2fт/3, а максимальная частота шумовой манипуляции, равная fт/5, на частотах модулятора 2fт/5 и 3fт/5.
    Последующее цифровое преобразование с частотой дискретизации fд = fт/2N сопровождается , ввиду фильтрующих свойств преобразования, ослаблением преобразуемого сигнала в области его верхних частот. Введение дополнительной передискретизации в сочетании с применяемой цифровой фильтрацией и децимацией обеспечивает выравнивание частотной характеристики преобразования.
    Сигма-дельта модуляторы высоких порядков обладают свойствами полиномиальных ФНЧ, что предъявляет дополнительные требования к параметрам их частотных характеристик.

Литература

• Sigma-Delta (S-D) A/D Converters // New Product Applications 1999, winter edition. Analog Devices, 1998, рp. 3-113 3-143.
  
• Application Note AN-283: Sigma-Delta ADCs and DACs // Applications Reference Manual. Analog Devices, 1993, рp. 20-3 20-18.
  
• Application Notes AN-388/AN-389: Using Sigma-Delta Converters // 1995 DSP/MSP Products Reference Manual. Analog Devices, 1995, рp. 6-47 6-59.
  
• Сигма-дельта АЦП фирмы Analog Devices // Электронные компоненты и системы. Киев: VD MAIS. Май 1996. C. 2025.
  
• Швец В., Нищирет Ю. Архитектура сигма-дельта АЦП и ЦАП // CHIP NEWS. 1998. ╧ 2. C. 211.
  
• Хоровиц П., Хилл У. Искусство схемотехники. Т. 2. М: Мир. 1983. C. 7275.
  
• Голуб В.С. Мгновенная и средняя частота колебаний и интегрирующие ЧМ и ЧИМ модуляторы // Радиотехника. 1982. ╧ 9. C. 4850.
  

НПФ "VD MAIS", Киев
Тел. (044) 227-1356, факс (044) 227-3668
E-mail: vdmais@carrier.kiev.ua
http://www.vdmais.kiev.ua