|
А. Гусев, Э. Лидский, О. Мироненко Малые выборки при оценке работоспособности и надежности электронных компонентов. Часть 1Понятие малая выборка не имеет универсального определения. Косвенно уровень малости выборки при испытаниях заложен в современной характеристике над╦жности FIT. Такое представление в значительной степени конъюнктурно. Предметная область применения малых выборок достаточно широка. К ней относятся испытания электронных компонентов в различных режимах в составе аппаратуры и другие работы, носящие исследовательский характер. Особенности возникают как при организации испытаний, так и при осмысливании результатов. В первой части статьи предлагается количественная оценка вероятности выхода измеряемого параметра за допустимый предел. Оценка строится на основе гипотезы о марковости процесса изменения состояния объекта. Испытания проводятся при малой выборке, возможно, как ускоренные. Приводится пример применения предложенной методики обработки полученных данных. Отмечается связь с упомянутой характеристикой FIT. Дан краткий обзор работ, связанных с малой выборкой. Характеристики над╦жности:
Малые выборки в статистикеПод выборкой ниже понимается либо число образцов, поставленных на испытания в заданном режиме, либо произведение числа образцов на время испытаний DH (Device Hours) [1]. Назначение объ╦ма выборки сопутствует циклу испытаний и статистическому анализу [2,3]. Один из основных вопросов математической статистики: какова должна быть минимально необходимая информация для получения требуемой достоверности результата. В частности, речь пойд╦т о числе образцов, поставленных на испытания при прочих равных условиях. Если подразумевать под условиями отсутствие каких-либо ограничений по точности конечного результата статистического анализа, то ответ на поставленный вопрос дал Р. Фишер [4,5]. Минимальное число образцов не может быть меньше 4. В противном случае, неизбежно возникает систематическая ошибка (смещение). Наличие смещения - первый признак отсутствия достаточности статистики [6]. Ряд авторов подтверждал вывод Фишера. Исследования, касающиеся малых выборок, связаны с именами А.Н. Колмогорова, Дж. Неймана и А. Вальда. А.Н. Колмогоров установил критерий достаточности статистики при ограниченном числе наблюдений [7]. Дж. Нейман [8] создал новое направление в статистике, основное положение которого гласит: "Задача статистики - выявлять общий характер поведения объекта в условиях неопредел╦нности". Такая позиция вполне согласуется с ограниченной возможностью делать слишком конкретные выводы при малых выборках. Идеи Дж. Неймана легли в основу Теории решений [6] - аппарата принятия гипотезы при явной неполноте информации. А. Вальд разработал раздел статистики, именуемый последовательным анализом [9]. Необходимый объ╦м выборки, под которым понимается DH, определяется в процессе самих испытаний. Теоретически последовательная процедура требует для принятия решения меньший объ╦м выборки, чем при заранее фиксированном DH. Реально, при малой выборке дискретность параметра может сказаться отрицательно. Поэтому к такому выводу следует подходить с осторожностью [10]. Идеи Колмогорова, Неймана и Вальда в части малых выборок развиты в большом числе последующих работ, библиографию которых можно найти в фундаментальных трудах по статистике (например [11,12]). В настоящее время прослеживается некоторое сужение области применения малых выборок при обработке результатов испытаний электронных компонентов (ЭК) [13]. Ведущие фирмы - изготовители ЭК при получении оценок над╦жности используют большие выборки [14-17]. Оценки типа FIT позволяют тогда сравнивать ЭК по разным классам изделий, технологиям, фирмам [18]. Задача испытаний и обработки результатов при малой выборке оста╦тся актуальной в случае:
Последнее сосредотачивает сегодня наибольшее число работ, связанных с малыми выборками, что естественно, так как классификация есть принятие решения при недостатке информации. К. Мартином и С. Хиршбергом дан весьма полный обзор работ, получены уточн╦нные формулы достоверности и доверительных интервалов, а также критерий применимости малых выборок [21,22]. Малая выборка при оценке надежностиКатастрофический отказ ЭК есть необратимая полная потеря работоспособности. Поэтому анализ над╦жности не связан с выбором специальных параметров, идентифицирующих уровень работоспособности. Целесообразно сначала рассмотреть предлагаемый метод получения оценок над╦жности при малой выборке, объединяя уровни работоспособности понятием "исправность" ЭК. Будем считать, что испытания проводятся по схеме ускоренных. Факторы ускорения: термическая нагрузка, или напряжение питания, или включение изделия в цепь с повышенным током, или, наконец, совместное действие перечисленных факторов. Ставятся следующие задачи:
Новое понимание цели расч╦тно-экспериментального оценивания над╦жности электронных компонентов подробно разобрано в [18]. Остановимся только на выводах, которые дают решение первой из поставленных задач [1]. По рекомендации ряда фирм производителей ЭК, интенсивность отказов определяется не для одного типа ЭК, а для целой группы ЭК, связанных единством технологии, или назначения, или фирменно. Экспериментальная интенсивность отказов FR (Failure Rate) записывается в виде
где: рассматривается как случайная величина, распредел╦нная по закону x²; Если считать, что за время испытаний отказов не зарегистрировано, то m = 2 и FR совпадает с традиционным представлением об интенсивности отказов при экспоненциальном распределении времени до наступления отказа. В противном случае, (1) основывается на факте, что число отказов мало и распределение не очень отличается от экспоненциального. Как будет видно из дальнейшего, ошибка при такой гипотезе не является особо существенной при использовании нетрадиционными показателями над╦жности. FIT (Failure in Time) есть число отказов за время EDH. FIT = FR╥109 (2) Запишем экспериментальную интенсивность отказов в известной для экспоненциального распределения форме
Умножая 5 < (n/EDH)x109 < 6. Таким образом, умножение на 109 имело цель установить FIT целым в пределах 0÷9 для всей продукции ADI. При таком подходе FIT становится сравнительной оценкой не только над╦жности как таковой, но и косвенной характеристикой гарантии фирмы на установленный срок службы прибора. Если, например FIT = 100, то это свидетельствует о недостаточной информации, полученной при испытаниях, - большом K = 109/EDH. Недостаток информации от испытаний - это и есть то, что свидетельствует о малости обобщ╦нной выборки EDH. Конечно, оста╦тся открытым вопрос о том, что следует понимать под малой, очень малой, сверхмалой и т.п. выборками. Прежде чем говорить о подобной градации, остановимся на способе получения информации - испытаниях ЭК. Как правило, испытания проводятся ускоренно [14], хотя есть также методики оценки над╦жности по результатам испытаний в нормальном режиме [23]. В [15] изложены варианты расч╦та множителя At при совместном действии повышенной температуры среды T (125÷150ºС) и повышенного напряжения питания Vcc. At(T,Vcc) = K1(T)K2(Vcc), где ea - энергия активации; B - постоянная Больцмана 8,618╥10-5eV/ºK; T(ºK) - температура при испытаниях; To(ºK) - номинальная температура; P (W) - рассеиваемая мощность; Po(W) - номинальная рассеиваемая мощность; K2(V) = exp{Z(Vcc √ Vccº)} (4) где Vcc(B) - напряжение при испытаниях (Vcc ~ 1,3Vºcc); Vºcc(B) - номинальное напряжение; Z (0,5÷1,0) - размерный коэффициент. Выражение для K1(T) хорошо известно и широко применяется. Вычисление K2(V) не так понятно. Удобство пользования (3) и (4) очевидно. Но существует ряд предложений, достаточно обоснованных [24-26], трактующих связь показателей над╦жности с напряжением питания иначе. Так, в [27] рекомендуется вычислять интенсивность отказов по формуле (при
где I - ток в контуре включения прибора при испытаниях, Io - номинальный ток. Показатели степени Вопрос о достоверности при малой выборке следует рассматривать в двух аспектах. Во-первых, допустимо ли при малой выборке пользоваться результатами ускоренных испытаний для оценки над╦жности (речь в данном случае не ид╦т о гарантиях фирм)? Во-вторых, как получить максимально возможную достоверность при прогнозе показателей над╦жности? Помимо этого, принимаемая методика прогноза должна быть увязана с новыми показателями FIT, MTTF = 109/FIT (Mean Time To Failure) - средняя наработка до отказа. Зарубежные источники избегают затрагивать вопросы, связанные с испытаниями при малых EDH. Считается, что если объ╦м испытаний мал (FIT >> 10), то прогноз над╦жности теряет смысл. Однако на практике выводы на основании таких испытаний делать приходится (табл. 1, 2, заимствованные из [16]). Таблица 1. Результаты испытаний
Таблица 2. Расч╦тные показатели надежности при разных температурах перехода
Изложим вкратце один подход к решению возникшей проблемы, подробно описанный в [28] и успешно применявшийся [29]. При этом модель процесса изменения технических параметров объекта просто связывается с принятой при построении FIT. Постоянство параметра FR в терминах случайных процессов означает, что рассматривается Марковский процесс с двумя состояниями, одно из которых (отказовое) является поглощающим. Представим состояние исправности в виде конечного множества n-1 состояний. Элемент множества - квант состояния - характеризуется значениями технических параметров объекта. Сохраним предположение о Марковском характере процесса перехода из состояния в состояние. Интенсивности переходов объединим в матрицу
Показывая только идею подхода, не останавливаемся на задаче получения матрицы (6) по результатам испытаний, хотя именно при е╦ решении возникают основные трудности. Подробно изложение метода можно найти в [30]. Вероятность отказа определяется системой уравнений [31]:
где Q(t|i) - вероятность отказа за время t при i-ом начальном состоянии. Прямое использование результатов испытаний в изложенном подходе не является возможным из-за малой выборки. Действительно, как правило, отказы будут отсутствовать (в противном случае, прогноз теряет смысл). В матрице (6) оценки наибольшего правдоподобия дают нулевой столбец В упоминавшихся работах предложен способ принятия решения для перехода от точечных оценок элементов матрицы (6) к интервальным. Тогда решение системы (7) переста╦т быть тривиальным, и подход может быть развит для практики. Для вычисления FIT отсутствие отказов не является препятствием. Покажем, как можно связать наблюдения в квантованном поле значений параметров объекта с показателями типа FR, FIT и MTTF. Введ╦м гипотезу наихудшего случая при фактически не наблюдавшихся отказах в процессе испытаний: любой уход из кванта состояния означает отказ. Другими словами, в новой матрице P* интенсивностей переходов pin* = pi: pi находится по результатам испытаний где mi - число уходов из кванта, Вероятность отказа за время t
Таким образом имеет место закон Пуассона для вероятности x отказов за время t
где N0(i) - число образцов в i-ом состоянии в момент t = 0. При применении распределения x² два очевидных равенства определяют число степеней свободы, равное 2: x + y = N0(i), где y - число не отказавших образцов, и В свою очередь, две степени свободы означают, что при испытаниях отказы не наблюдались. Аналог (1) записывается в виде
Определим FR для ЭК как
Вычисление FIT производится согласно (2). Пример. Испытания транзистора 2Т828. Параметр: h21. x²1√0,6(18) = 16,257, FIT = FR╥109 = 0,387╥105 1/ч, Гарантируемая наработка до отказа много меньше полного времени испытаний. Сравнительно большое число переходов из кванта в квант свидетельствует об известной нестабильности технического параметра, что заставляет предполагать существенной вероятность ухода его значений за допустимые пределы. Показатель FIT >> 10. Выборка может считаться очень малой. Расч╦т этого примера по методике [30] да╦т вероятность отказа за 30000 час равную 0,0186. Если принять (только для сравнения c примером!) экспоненциальное распределение времени до отказа, то интенсивность отказов l будет равна 0,625╥10-6 1/ч. Разница между FR и Напомним, что множитель 109 достаточно произволен и отражает конъюнктуру рынка, а не физические свойства. Вероятно было бы уместно ввести иное наименование для FIT, так как Failure in Time сохраняет перевод "интенсивность отказов" [33]. Вместе с тем, FIT есть удобная сравнительная характеристика, оценивающая неполноту информации об объекте, полученной при проведении испытаний. Литература
|


 Малые выборки при оценке работоспособности и надежности электронных компонентов. Часть 1
Малые выборки при оценке работоспособности и надежности электронных компонентов. Часть 1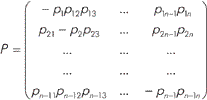 (6)
(6)