В. Соловьев, А. Климович

Синтез на ПЛИС одноуровневых комбинационных схем

Рассматриваются два метода синтеза одноуровневых комбинационных схем на ПЛИС: без использования монтажного соединения выходов (метод М1) и в случае использования монтажного соединения выходов для реализации функции "ИЛИ" (метод М2). Указываются отличия методов для тр╦х архитектурных моделей ПЛИС: "классических" PAL, универсальных PAL и CPLD. Провед╦нные экспериментальные исследования показали высокую эффективность метода М2, который, по сравнению с методами пакета MAX+PLUSII, позволяет для отдельных примеров снизить стоимость реализации более чем в 25 раз, а быстродействие повысить в 15 раз. Отмечаются положительные и отрицательные качества каждого из методов, а также области их наиболее эффективного использования.

Введение

Под одноуровневой комбинационной схемой на ПЛИС понимается комбинационная схема, в которой сигналы на пути со входов на выходы схемы не проходят через скрытые макроячейки и только один раз проходят через выходные макроячейки ПЛИС.

Одноуровневые комбинационные схемы заслуженно пользуются большой популярностью среди разработчиков цифровых систем благодаря своей простоте и высокому быстродействию. Кроме того, все выходные сигналы в одноуровневых схемах имеют одну и ту же временную задержку. В общем случае возможны два подхода к синтезу одноуровневых комбинационных схем на ПЛИС: когда допускается монтажное соединение выходов ПЛИС по ИЛИ и когда монтажное соединение выходов запрещено. В предлагаемых методах синтеза рассматриваются три архитектурные модели ПЛИС: "классические" PAL (Programmable Array Logic), универсальные PAL и CPLD (Complex Programmable Logic Device) [1].

"Классические" PAL характеризуются числом входов n, числом выходных макроячеек m и числом q промежуточных шин, подсоединяемых к каждой макроячейке. Универсальные PAL характеризуются числом входов n, числом выходных макроячеек с одной обратной связью m, числом выходных макроячеек с двумя обратными связями m2, а также множеством Q = {q₁,...,q_k}, где q_s - число промежуточных шин, подсоединяемых к макроячейке MC_s, q_s € Q, s = ¯1,¯k, k = m + m₂. Функциональный блок CPLD характеризуется числом входов n, выходных макроячеек m, суммарным числом промежуточных шин функционального блока q_e и максимальным числом промежуточных шин q_max, которые могут быть подсоединены к одной макроячейке.

Пусть комбинационная схема задана системой булевых функций (СБФ), представленных в дизъюнктивной нормальной форме (ДНФ). СБФ будем характеризовать числом N выходных функций (выходных переменных) множества Y = {y₁,...,y_N} и числом L аргументов функций (входных переменных) множества X = {x₁,...,x_L}. Кроме того, каждая функция y_i характеризуется числом Q(y_i) слагаемых (элементарных конъюнкций) в ДНФ функции y_i, y_i € Y.

Предлагаемые методы синтеза одноуровневых комбинационных схем на ПЛИС включают два этапа: на первом этапе определяется множество Y* реализуемых функций, на втором этапе выполняется разбиение множества Y* на минимальное число T подмножеств Y₁,...,Y_T таким образом, чтобы каждое подмножество Y_t, t = ¯1,¯T, допускало реализацию на t-й PAL (функциональном блоке CPLD). При описании методов синтеза вначале приводится метод синтеза на универсальных PAL, а затем метод уточняется для "классических" PAL и CPLD.

Синтез одноуровневых комбинационных схем без использования монтажного соединения выходов ПЛИС по ИЛИ (метод М1)

При построении одноуровневых комбинационных схем на универсальных PAL главным препятствием является ограничение на число промежуточных шин, подсоединяемых к одной макроячейке. С другой стороны, поскольку универсальные PAL позволяют программировать уровень активности (высокий или низкий) логического сигнала каждого выхода, можно реализовать прямое или инверсное представление каждой функции y_i, y_i € Y, в зависимости от того, какое из значений меньше - Q(y_i) или Q(¯y_i). Синтез усложняется также тем, что с различными макроячейками универсальных PAL связано различное число промежуточных шин.

Необходимыми и достаточными условиями реализации СБФ Y одноуровневой схемой на универсальных PAL является выполнение неравенств:

|X(ý_i)| n + k √ 1, (1)
Q(ý_i) q_max для всех i = ¯1,¯N,

где X(ý_i) - число аргументов функции ý_i; ý_i - одна из функций y_i или ¯y_i; q_max - максимальный элемент множества Q.

На первом этапе синтеза в множество Y* из двух функций y_i и ¯y_i, i = ¯1,¯N, выбирается функция, для которой выполняются условия (1) и значение Q(ý_i) для которой меньше.

На втором этапе синтеза решается следующая задача.

Задача 1

Разбить множество Y* на минимальное число T подмножеств Y₁,...,Y_T таким образом, чтобы для каждого подмножества выполнялись условия:

|Y_t| k;
|X_t| n + k √ |Y_t|, t = ¯1,­T,

а также, чтобы для каждой функции y_i, y_i € Y, нашлось значение q_s, q_s € Q, такое, что

Q(ý_i) q_s, (2)

прич╦м различным функциям ý_i, ý_i € Y*, должны соответствовать различные значения q_s, q_s О Q, где X_t - множество аргументов функций подмножества Y_t, t = ¯1,¯T.

Алгоритм решения задачи 1 имеет вид.

Алгоритм 1

1. Полагается t := 0.
2. Полагается t := t + 1, Q* := Q. Начинается формирование подмножества Y_t.

   В качестве опорного элемента в подмножество Y_t выбирается функция ý_i, ý_i € Y*, для которой |X(ý_i)| = _max; если таких функций несколько, то среди них выбирается функция, для которой Q(ý_i) = _max.

   Для реализации функции y_i в t-й PAL определяется макроячейка MCs, для которой выполняется условие (2), q_s € Q*; если таких макроячеек несколько, то среди них выбирается макроячейка с минимальным значением q_s.

   Полагается: Y_t := {ý_i}; X_t := Xýy_i); Q* := := Q*\{q_s}; Y* := Y*\{ý_i}; Q_t := Q(ý_i), где Q_t - суммарное число промежуточных шин, необходимое для реализации функций множества Y_t.

3. Осуществляется добавление элементов в множество Y_t. Для этого находится функция ý_i, ý_i € Y*, для которой выполняются условия

   |Y_t| + 1 k;
   |X_t X(y_i)| n + k √ |Y_t| √ 1; (3)
   Q(ý_i) q_s,

   где q_s - число промежуточных шин, подсоедин╦нных к некоторой незадействованной макроячейке PAL, q_s € Q.

   q_eсли таких функций несколько, то среди них выбирается функция, для которой |X_t X(ý_i)| = _max, а среди них функция, для которой |X(ý_i)\X_t| = min. Функции y_i назначается для реализации s-я макроячейка t-й PAL аналогично тому, как это выполнялось в пункте 2.

   Полагается:
   Y_t:= Y_t {ý_i};
   X_t := X_t X(ý_i);
   Q* := Q*\{q_s};
   Y* := Y*\{ý_i};
   Q_t := Q_t + Q(ý_i).

   Пункт 3 повторяется до тех пор, пока в множество Y_t может быть включена хотя бы одна функция.

4. q_eсли Y , выполняется переход к пункту 2, иначе - к пункту 5.
5. Конец.

Пример 1

Пусть универсальные PAL имеют следующие параметры: n = 3, m = 2, m₂ = 1 и Q = {1,2,4}, а СБФ Y задана следующими логическими уравнениями:

y₁ = ¯x₁ + x₅ + x₆ + x₈;
y₂ = ¯x₁╥x¯₆ + x₁╥x₆ + ¯x₅╥x₆╥¯x₈ + x₅╥¯x₆╥¯x₈ + + x₁╥¯x₅╥x₈ + x₅╥x₆╥x₈;
y₃ = ¯x₂╥¯x₃ + x₂╥x₃ + ¯x₇╥¯x₉ + ¯x₂╥x₇ + x₂╥x₉;
y₄ = ¯x₇╥¯x₉ + ¯x₂╥¯x₃╥¯x₇ + x₂╥¯x₃╥x₉ + x₃╥x₇ + ¯x₂╥x₇╥¯x₉;
y₅ = ¯x₄ + x₅ + x₇;
y₆ = x₄╥¯x₅ + x¯₄╥x₅ + ¯x₇;
y₇ = x₄╥¯x₅ + ¯x₄╥x₅ + x₅╥x₇ + ¯x₅╥¯x₇;
y₈ = ¯x₅╥¯x₆╥¯x₇ + ¯x₇╥¯x₈╥¯x₉ + x₅╥x₆╥¯x₇ + ¯x₅╥¯x₇╥x₈ + x₅╥¯x₇╥x₉ + x₇╥x₈╥¯x₉ + ¯x₅╥x₆╥x₇ + x₅╥¯x₆╥x₇ + ¯x₅╥x₇╥x₉ + x₅╥x₇╥¯x₈.

Инверсии функций имеют следующий вид:

¯y₁ = x₁╥¯x₅╥¯x₆╥¯x₈;
¯y₂ = x₁╥¯x₅╥¯x₆╥¯x₈ + x₁╥x₅╥¯x₆╥x₈ + ¯x₁╥¯x₅╥x₆╥x₈ + ¯x₁╥x₅╥x₆╥¯x₈;
¯y₃ = ¯x₂╥x₃╥¯x₇╥x₉ + x₂╥¯x₃╥x₇╥¯x₉;
¯y₄ = x₃╥¯x₇╥x₉ + ¯x₂╥¯x₃╥x₇╥x₉ + x₂╥¯x₃╥x₇╥¯x₉;
¯y₅ = x₄╥¯x₅╥¯x₇;
¯y₆ = ¯x₄╥¯x₅╥x₇ + x₄╥x₅╥x₇;
¯y₇ = ¯x₄╥¯x₅╥¯x₇ + x₄╥x₅╥¯x₇;
¯y₈ = ¯x₅╥x₆╥¯x₇╥¯x₈╥x₉ + x₅╥¯x₆╥¯x₇╥x₈╥x₉ + x₅╥x₆╥x₇╥x₈╥x₉ + ¯x₅╥¯x₆╥x₇╥¯x₈╥¯x₉.

Исходные данные для работы алгоритма 1 представлены в табл. 1. Поскольку для всех функций справедливо Q(¯y_i) < Q(y_i), то в множество Y* включаются только инверсные представления функций.

Таблица 1. Исходные данные для работы алгоритма 1

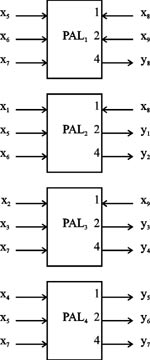
В соответствии с пунктом 2 алгоритма 1, первым в множество Y₁ включается функция ¯y₈, так как только для этой функции |X(¯y₈)| = 5 = _max. На этом формирование множества Y₁ заканчивается, поскольку нельзя добавить ни одной функции из-за нарушения условий (3).

В качестве опорного элемента множества Y₂ выбирается функция ¯y₂, затем в множество Y₂ добавляется единственная функция ¯y₁. Аналогично формируются множества Y₃ и Y₄. Окончательная реализация СБФ показана на рис. 1. Здесь возле каждого вывода записано число промежуточных шин, связанных с соответствующей макроячейкой.

Рисунок 1. Реализация СБФ из примера 1 одноуровневой схемой на универсальных PAL без использования монтажного объединения выходов по ИЛИ

Необходимые и достаточные условия реализации СБФ Y на "классических" PAL имеют вид:

|X(y_i)| n + m √ 1;
Q(y_i) q, для всех i = ¯1,¯N.

q_eсли принять k := m, q_s := q и Y* := Y, то метод М1 для "классических" PAL полностью совпадает с методом М1 для универсальных PAL.

Необходимым и достаточным условием возможности реализации СБФ Y одноуровневой схемой на CPLD является выполнение неравенств:

|X(ý_i)| n;
Q(ý_i) q_max, для всех i = ¯1,¯N.

Реализация СБФ Y* одноуровневой комбинационной схемы на CPLD сводится к разбиению множество Y* на минимальное число T подмножеств Y₁,...,Y_T таким образом, чтобы для каждого подмножества выполнялись условия:

|Y_t| m;
|X_t| n;
Q_t q_e, для всех t = ¯1,¯T.

Некоторая функция y_i, y_i € Y*, может быть добавлена в подмножество Y_t, t = ¯1,¯T, если выполняются условия:

|Y_t|+ 1 m;
|X_t И X(y_i)| n; (4)
Q_t + Q(y_i) q_e.

Метод М1 синтеза одноуровневой комбинационной схемы на CPLD аналогичен методу М1 для универсальных PAL, только в пункте 3 алгоритма 1 вместо условий (3) учитываются условия (4), а также отпадает необходимость в выборе макроячейки для реализации конкретной функции, так как все выходные макроячейки CPLD равнозначны.

Синтез одноуровневых комбинационных схем с использованием монтажного соединения выходов ПЛИС по ИЛИ (метод М2)

Многие ПЛИС допускают монтажное объединение внешних выводов с целью реализации логической функции ИЛИ. Для возможности такого объединения выходные буферы ПЛИС должны быть изготовлены по технологии с открытым коллектором или обладать свойством программирования открытого стока (open-drain) для каждого выхода.

Необходимым и достаточным условием реализации СБФ Y на универсальных PAL с использованием монтажного объединения выходов по ИЛИ является выполнение неравенств:

r(y_i) n + k √ 1 для всех i = ¯1,¯N,

где r(¯y_i) - максимальный ранг (число литералов) конъюнкций в представлении функции ¯y_i, i = ¯1,¯N.

В качестве реализуемых функций принимается множество Y* = {¯y₁,...,¯y_N}, поскольку монтажное ИЛИ реализуется только в инверсной логике.

СБФ Y* представим в виде двух матриц: троичной А и булевой В. Матрицы А и В имеют одинаковое число строк, соответствующих элементарным конъюнкциям k₁,...,k_P. Столбцы матрицы А соответствуют аргументам, а матрицы В - функциям множества Y. На пересечении строки i и столбца j матрицы А ставится единица, если входная переменная x_j, x_j € X, входит в i-ю конъюнкцию в прямом значении, ноль - в инверсном значении и прочерк ("√"), если x_j не входит в i-ю конъюнкцию. На пересечении строки i и столбца j матрицы В ставится единица, если i-я конъюнкция входит в ДНФ функции y_j, y_j € Y. Каждой строке матрицы B поставим в соответствие множество X(k_i) аргументов, имеющих в строке i матрицы A значения, отличные от безразличных, i = ¯1,¯P. На втором этапе синтеза решается следующая задача.

Задача 2

Покрыть матрицу B минимальным числом T миноров B₁,...,B_T таким образом, чтобы для каждого минора выполнялись условия:

|Y_t| k;
|X_t| n + k √ |Y_t|, t = ¯1,¯T,

а также для каждого столбца j минора B_T нашлось значение q_s, q_s € Q, такое, что выполняется

Q_j^t q_s,

прич╦м различным столбцам минора B_T должны соответствовать различные значения q_s, q_s € Q, где Y_t - множество функций, соответствующих столбцам минора B_T; X_t - множество аргументов, соответствующих строкам минора B_T; K_t - множество конъюнкций, соответствующих строкам минора B_T; Q_j^t - число единиц в столбце j минора B_T, t = ¯1,¯T.

Решение задачи 2 выглядит следующим образом.

Алгоритм 2

1. Полагается t := 0.
2. Полагается
   t := t + 1;
   Q* := Q;
   Q_j^t := 0 для всех j = ¯1,¯N.

   Начинается формирование очередного минора B_T. В качестве опорных в минор B_T включается строка i и столбец j, имеющие общую единицу, такие, что для строки i выполняется

   |X(k_i)| = _max,

   а столбец j содержит максимальное число единиц. q_eсли таких пар (i,j) строк и столбцов может быть выбрано несколько, то среди них выбирается строка i и столбец j с максимальным суммарным числом единиц.

   Выбранные строка i и столбец j включаются в минор B_T, полагается: K_t := {k_i}; X_t := X(k_i); Y_t := {y_j}; Q_j^t := 1; Q_t := 1.

3. Осуществляется покрытие единиц матрицы B минором B_T. Для этого в матрице B находится единица на пересечении строки i и столбца j, для которой выполняются условия
   

   |Y_t {y_j}| k;
   |X_t X(k_i)| n + k √ |Y_t {y_j}|, (5)

   а также, если среди свободных макроячеек t-й PAL найд╦тся макроячейка с числом промежуточных шин q_s такая, что выполняется неравенство:

   Q_j^t + 1 q_s. (6)

   При наличии альтернативы выбора предпочтение отда╦тся единице, для которой

   |X_t X(k_i)| = _max,

   а среди них - единице, для которой

   |X(k_i)\X_t| = min.

   В случае равных возможностей выбора предпосылка отда╦тся единице, расположенной в столбцах минора B_T.

   Строка i и столбец j, на пересечении которых находится выбранная единица, включается в минор B_T, полагается:

   K_t := K_t {k_i};
   Y_t := Y_t {y_j};
   X_t := X_t X(k_i);
   Q_t := Q_t + 1.

   Пункт 3 повторяется до тех пор, пока минором B_T может быть покрыта хотя бы одна единица матрицы B.

4. Выполняется назначение макроячеек PAL реализуемым функциям. Для каждой функции y_j, y_j € Y_t, среди свободных макроячеек PAL с числом промежуточных шин, удовлетворяющих условию (6), выбирается макроячейка с минимальным значением q_s. Функция y_j, y_j € Y_t, назначается для реализации на s-ю макроячейку t-й PAL, полагается

   Q_j^t := Q_j^t + 1;
   Q* := Q*\{q_s}.

   В матрице В исключаются единицы, покрытые минором B_t. Если в матрице B остались непокрытые единицы, то выполняется переход к пункту 2; иначе выполняется переход к пункту 5.

5. Конец.

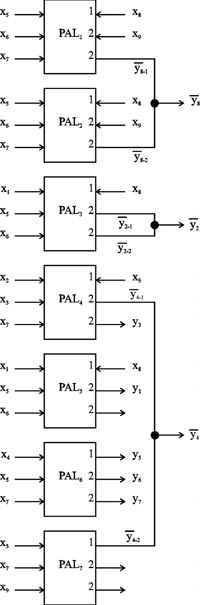
Пример 2

Работу алгоритма 2 рассмотрим на примере синтеза комбинационной схемы, заданной СБФ из примера 1 на универсальной PAL со следующими параметрами: n = 3, m = 2, mБыгиЮ2 = 1 и Q = = {1,2,2}. Отметим, что реализация СБФ Y* на PAL с заданными параметрами с помощью метода М1 невозможна.

Матрицы A и B реализуемой СБФ Y* приведены в табл. 2. В соответствии с пунктом 2 алгоритма 2 в качестве опорных в минор B₁ включаются строка 15 и столбец 8, то есть пара (15,8), так как |X(k₁₅)| = 5 = max и столбец 8 содержит максимальное число единиц. Затем минором B₁ покрывается единица, соответствующая паре (16,8). На этом формирование минора B₁ заканчивается из-за нарушения условий (5). Аналогичным образом формируются миноры B₂,...,B₇. Результаты выполнения алгоритма и формируемые при этом значения приведены в табл. 3. Монтажными соединениями выходы PAL объединяются так, как показано на рис. 2.

Таблица 2. Реализуемая СБФ из примера 2

Таблица 3. Результаты выполнения алгоритма 2

Рисунок 2. Реализация СБФ из примера 2 одноуровневой схемой на универсальных PAL с использованием монтажного объединения выходов по ИЛИ

Если принять k := m, а также q_s := q для всех q_s, q_s € Q, то метод М2 на универсальных PAL может быть примен╦н для синтеза комбинационных схем на "классических" PAL.

Необходимым и достаточным условием реализации СБФ Y на CPLD с использованием монтажного объединения выходов по ИЛИ является выполнение неравенств:

r(¯y_i) n для всех i = ¯1,¯N,

где n - число входов функционального блока CPLD.

Задача синтеза комбинационных схем на CPLD с помощью метода М2 сводится к покрытию матрицы B минимальным числом T миноров B₁,...,B_t таким образом, чтобы для каждого минора выполнялись условия:

|Y_t| m;
|X_t| n;
Q_t q_s, t = ¯1,¯T,

а также для каждого столбца j минора B_t выполнялось

Q_j^t q_max.

При построении очередного минора B_t, t = ¯1,¯T, некоторая единица матрицы B на пересечении строки i и столбца j может быть покрыта минором Bt при выполнении неравенств:

|Y_t {y_j}| m;
|X_t X(k_i)| n; (7)
Q_t + 1 q,

а также, если выполняется неравенство:

Q_j^t + 1 q_max. (8)

Алгоритм синтеза комбинационных схем на CPLD с использованием монтажного соединения выходов по ИЛИ совпадает с алгоритмом 2, за исключением того, что в пункте 3 вместо условий (5) и (6) рассматриваются условия (7) и (8).

Результаты экспериментальных исследований

Методы М1 и М2 реализованы программно в пакете ZUBR. В качестве эталонных примеров для проверки предлагаемых методов синтеза использовались комбинационные схемы, разработанные в центре MCNC [2]. Предложенные методы М1 и М2 синтеза одноуровневых комбинационных схем сравнивались с методами синтеза, реализованными в пакете MAX+PLUSII версии 10.1 фирмы Altera. В качестве ПЛИС рассматривались универсальные PAL семейства CLASSIC, CPLD семейства MAX 7000, а также FPGA семейства FLEX 10K.

Результаты синтеза оценивались по двум параметрам: стоимости и быстродействию. В качестве стоимости было принято число макроячеек ПЛИС, затрачиваемых на реализацию комбинационной схемы, а в качестве быстродействия принята максимальная задержка прохождения сигналов со входа на выход синтезированной схемы.

Параметры логического синтеза пакета MAX+PLUSII были настроены на минимизацию стоимости (Global Project Synthesis Style: NORMAL; Optimize: Area), при этом допускалось использование всех архитектурных особенностей каждого семейства (Automatic Open-Drain Pins: ON; Minimization: Full; XOR Synthesis: ON; Parallel Expanders: ON; Automatic Implement in EAB: ON; Carry Chain: Auto; Cascade Chain: Auto; Advanced Options: все ON). Поскольку синтезировались одноуровневые схемы, параметр Multi-level Synthesis был установлен в OFF.

Провед╦нные экспериментальные исследования метода М1 показали, что данный метод имеет малую область использования (около 10% для всех эталонных примеров) из-за нарушения необходимых и достаточных условий применения, а для тех примеров, где метод М1 применим, результаты совпадают с результатами, полученными с помощью пакета MAX+PLUSII.

Результаты экспериментальных исследований метода М2, в сравнении с методами синтеза пакета MAX+PLUSII, приведены в табл. 4, 5 и 6 для ПЛИС семейств CLASSIC, MAX 7000 и FLEX 10K, соответственно, где C_A - стоимость реализации СБФ с помощью метода пакета MAX+PLUSII; C₂ - стоимость реализации СБФ с помощью метода М2; C_A/C₂ - отношение C_A к C₂; D_A - максимальная задержка, измеряемая в наносекундах, прохождения сигналов со входа на выход комбинационной схемы, синтезированной с помощью метода пакета MAX+PLUSII; D₂ - то же, но для комбинационной схемы, синтезированной с помощью метода М2; D_A/D₂ - отношение D_A к D₂.

Таблица 4. Результаты сравнения метода М2 с методом пакета MAX+PLUSII для семейства CLASSIC

Name	L	N	P	CA	C2	CA/C2	DA	D2	DA/D2
9sym	9	11	87	27	9	3,00	44	20	2,2
Alu4	14	8	1028	554	66	8,40	270	20	13,5
Apex1	45	45	206	(1)	196	-	(1)	22	-
Apex2	39	3	1035	(1)	57	-	(1)	22	-
Apex3	54	50	280	333	113	2,95	108	22	4,91
Apex4	9	19	438	564	141	4,00	106	20	5,3
B12	15	9	431	9	9	1,00	20	20	1,00
Cps	24	109	654	235	161	1,46	44	22	2,00
Ex1010	10	10	1024	770	117	6,58	304	20	15,2
Inc	7	9	34	14	11	1,27	32	20	1,6
Pdc	16	40	1280	(1)	48	-	(1)	20	-
Seq	41	35	1459	407	233	1,75	122	22	5,55
Table3	14	14	175	114	128	0,89	54	20	2,7
Table5	17	15	158	101	140	0,72	42	22	1,91
Z9sym	9	1	420	230	9	25,56	272	20	13,6
					1438	57,58		312	69,47
mid					95,87	4,80		20,8	5,79

(1) - синтез невозможен.

Таблица 5. Результаты сравнения метода М2 с методом пакета MAX+PLUSII для семейства MAX 7000

Name	L	N	P	CA	C2	CA/C2	DA	D2	DA/D2
9sym	9	1	87	20	15	1,33	15,5	6	2,58
Alu4	14	8	1028	143	116	1,23	51,5	12,5	4,12
Apex1	45	45	206	228	325	0,70	50,7	20	2,54
Apex2	39	3	1035	(1)	96	-	(1)	12,5	-
Apex3	54	50	280	316	168	1,88	37,5	15	2,50
Apex4	9	19	438	252	220	1,15	79,9	12,5	6,39
B12	15	9	431	9	11	0,82	9,5	9,5	1,00
Cps	24	109	654	(1)	245	-	(1)	20	-
Ex1010	10	10	1024	239	182	1,31	102,3	7,5	13,64
Inc	7	9	34	15	15	1,00	9,5	9,5	1,00
Pdc	16	40	1280	(1)	6	-	(1)	12,5	-
Seq	41	35	1459	246	403	0,61	68,2	20	3,41
Table3	14	14	175	125	205	0,61	19,9	12,5	1,59
Table5	17	15	158	115	274	0,42	44,9	12,5	3,59
Z9sym	9	1	420	22	15	1,47	31,6	6	5,27
					2356	12,53		188,5	47,63
mid					157,07	1,04		12,57	3,97

Таблица 6. Таблица 6. Результаты сравнения метода М2 с методом пакета MAX+PLUSII для семейства FLEX 10K

Name	L	N	P	CA	C2	CA/C2	DA	D2	DA/D2
9sym	9	1	87	87	59	1,48	33	20,2	1,63
Alu4	14	8	1028	535	540	0,99	46,2	33,1	1,40
Apex1	45	45	206	947	1378	0,69	49,6	76,9	0,64
Apex2	39	3	1035	141	335	0,42	40,6	37,1	1,09
Apex3	54	50	280	701	738	0,95	43,8	41,6	1,05
Apex4	9	19	438	1002	1141	0,88	52,8	42,9	1,23
B12	15	9	431	24	20	1,20	19,9	16,5	1,21
Cps	24	109	654	1484	751	1,98	57	59,3	0,96
Ex1010	10	10	1024	(1)	1126	-	(1)	45,4	-
Inc	7	9	34	40	36	1,11	22,8	19	1,20
Pdc	16	40	1280	534	164	3,26	48,4	25,5	1,90
Seq	41	35	1459	859	1612	0,53	51,9	101	0,51
Table3	14	14	175	744	963	0,77	52,7	40,2	1,31
Table5	17	15	158	636	1103	0,58	49,1	44,6	1,10
Z9sym	9	1	420	109	59	1,85	38,1	20,2	1,89
					10025	16,69		623,5	17,12
mid					668,33	1,19		41,57	1,22

Анализ полученных результатов показывает, что применение метода М2, по сравнению с методом пакета MAX+PLUSII, при синтезе комбинационных схем на ПЛИС семейства CLASSIC (табл. 4) позволяет значительно снизить стоимость реализации (в среднем, в 4,8 раза, а для отдельных примеров - в 25,5 раза) и значительно повысить быстродействие (в среднем, в 5,79 раза, а для отдельных примеров - в 15,2 раза).

Для семейства MAX 7000 (табл. 5) метод М2, по сравнению с методом пакета MAX+PLUSII, обеспечивает примерно одинаковую стоимость реализации (снижение стоимости, в среднем, составляет 1,04 раза, а для отдельных примеров - в 1,88 раза), однако позволяет значительно повысить быстродействие (в среднем, в 3,97 раза, а для отдельных примеров - в 13,64 раза).

Применение метода М2 при синтезе комбинационных схем на ПЛИС семейства FLEX 10K (табл. 6) позволяет, по сравнению с методом пакета MAX+PLUSII, как снизить стоимость (в среднем, в 1,19 раза, а для отдельных примеров - в 3,26 раза), так и повысить быстродействие (в среднем, в 1,22 раза, а для отдельных примеров - в 1,9 раза).

Выводы

1. Методу М1 присущи следующие положительные качества:
   • строятся комбинационные схемы максимального быстродействия, ограничиваемого только временем прохождения сигналов со входов на выходы ПЛИС;
   • все выходные сигналы имеют одинаковое время формирования;
   • метод позволяет применять раздельную минимизацию системы булевых функций, качество которой выше, чем совместная минимизация;
   • метод применим в цифровых системах как с прямой, так и с инверсной логикой;
   • для реализации СБФ требуется минимальное число макроячеек ПЛИС, равное числу реализуемых функций.
2. К недостаткам метода М1 можно отнести:
   • метод применим только к достаточно простым СБФ;
   • высокая общая стоимость реализации СБФ по числу используемых PAL или функциональных блоков CPLD.
3. Метод М1 наиболее эффективен при синтезе относительно простых комбинационных схем для любых классов ПЛИС в цифровых системах как с прямой, так и с инверсной логикой.
4. Положительными качествами метода М2 являются следующие:
   • строятся комбинационные схемы высокого быстродействия, отличающегося от метода М1 только задержкой на монтажном соединении выходов;
   • время формирования различных выходных сигналов отличается незначительно: на время задержки на монтажном соединении выходов;
   • метод позволяет применять раздельную минимизацию СБФ;
   • значительно более широкая область использования, по сравнению с методом М1.
5. К недостаткам метода М2 относятся следующие:
   • ПЛИС должны быть изготовлены по технологии с открытым коллектором или поддерживать программируемую опцию "открытый сток";
   • метод применим, в основном, в системах с инверсной логикой;
   • инверсное представление функций может быть значительно сложнее их прямого представления;
   • метод предусматривает последующее монтажное соединение выходов и установку для каждого монтажного соединения "подтягивающего" (pull-up) резистора, что может значительно усложнить этап конструкторского проектирования.
6. Метод М2 наиболее эффективен при синтезе достаточно сложных комбинационных схем в цифровых системах с инверсной логикой на ПЛИС, поддерживающих программируемые опции open-drain и pull-up.
7. Экспериментальные исследования показали, что применение метода М1 не позволяет улучшать стоимость и быстродействие синтезируемых комбинационных схем, по сравнению с методами, реализованными в пакете MAX+PLUSII.
8. Использование метода М2 позволяет значительно, по сравнению с методами, реализованными в пакете MAX+PLUSII, снизить стоимость реализации (до 25,5 раза) и повысить быстродействие (до 15,2 раза) синтезируемых комбинационных схем.
9. Метод М2 эффективен не только для ПЛИС со структурой двух программируемых матриц, но и для ПЛИС со структурой FPGA, что доказывается экспериментальными исследованиями для семейства FLEX 10K.

Литература

1. Соловьев В.В., Климович А. Введение в проектирование на ПЛИС комбинационных схем // Chip News. 2003. ╧ 5. С. 16√22.
2. Yang S. Logic synthesis and optimization benchmarks user guide. Version 3.0. Technical Report, Microelectronics Center of North Carolina, 1991. 43 p.