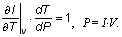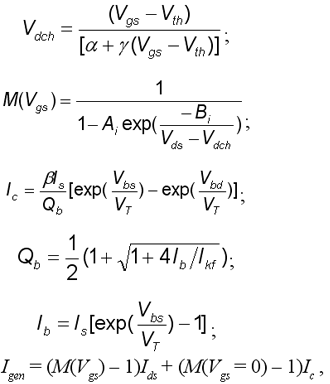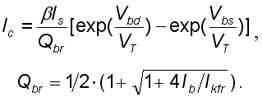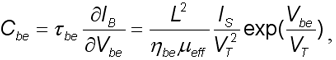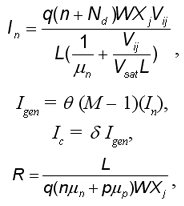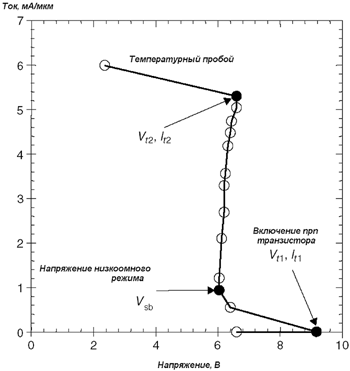
С. Волков, А. Ефишин, С. Морозов, С. Соколов

Проблема электростатического разряда и современные методы защиты интегральных схем от него. Часть 3.

Моделирование элементов защиты от ESD

Аналитические модели описания поведения полупроводниковых структур под воздействием ESD

Для точного описания работы полупроводниковых элементов под воздействием ESD необходимо охарактеризовать их поведение при больших токах инжекции. В существующих защитных схемах наиболее часто используются механизмы включения элемента с помощью паразитного латерального биполярного транзистора (КМОП-технология) и паразитного вертикального биполярного транзистора (БиКМОП и биполярная технологии) [1]. Во время ESD оба эти элемента работают в двухфазном режиме. Сначала, вследствие повышения напряжения на стоке МОП-транзистора, лавинная генерация дырок обеспечивает базовый ток, необходимый для включения npn-транзистора (рис. 1). Это происходит в точке (V_t1, I_t1). Паразитный биполярный транзистор проводит ток между коллектором и эмиттером с сопротивлением порядка нескольких Ом (режим snapback). В зависимости от технологии и типа защитной схемы, напряжение на стоке V_sb составляет несколько вольт, большая его часть падает на переходе база√коллектор, обеспечивая лавинную генерацию носителей. Почти вся мощность генерируется на переходе база√коллектор, поэтому понижение напряжения на этом переходе снижает выделение тепла в устройстве и позволяет элементу проводить больший ток. Ток I_t2 является максимальным стрессовым током, который может проводить устройство. На таком механизме отвода токов основано большинство схем защиты от ESD.

Рисунок 1. ВАХ nМОП-транзистора в режиме больших токов

В режиме больших токов выделяемое в устройстве тепло приводит к повышению внутренней температуры. Когда она достигает точки плавления кремния, элемент получает необратимые повреждения. Известно, что тепловой пробой, следующий за лавинным пробоем, возникает при температурах, меньших точки плавления. Как показано на рис. 1, ВАХ устройства после второго пробоя (V_t2, I_t2) резко изменяется. Параметры второго пробоя можно считать условиями отказа устройства. Так как второй пробой происходит в устройстве из-за повышения температуры, то основной целью при его моделировании является исследование роста температуры.

Как видно из ВАХ, после второго пробоя следует участок с отрицательным дифференциальным сопротивлением. В этом режиме напряжение и ток нестабильны, и напряжение уменьшается до тех пор, пока не будет выполнено условие стабильности. Когда это условие выполняется, весь ток протекает через небольшой участок элемента защиты. Таким образом, плотность тока в этом месте резко возрастает, и как следствие, резко возрастает температура. Поэтому для моделирования поведения защитных структур необходимо точное описание теплового пробоя.

В качестве критерия теплового пробоя в полупроводниковой структуре, обычно принимается достижение переходом база√коллектор температуры T_i, при которой концентрация собственных носителей (n_i) становится равной концентрации легирующей примеси (N_D). При выполнении этого условия положительный температурный коэффициент сопротивления становится отрицательным [1]. Однако использование T_i в качестве точного условия достижения второго пробоя в структурах, подверженных ESD, невозможно, так как в момент теплового пробоя n_i гораздо больше N_D из-за лавинной генерации.

Для более точного определения условий теплового пробоя в структурах защиты от ESD необходимо рассмотреть ток в устройстве как функцию напряжения и температуры. В этом случае получаем следующие условия пробоя [1]:

Однако это выражение непросто использовать в качестве условия определения второго пробоя из-за нелинейности уравнений, описывающих токи лавинной и температурной генерации. Отмеченная сложность обуславливает использование различных подходов к моделированию рассматриваемого явления.

Аналитическая модель, использующая уравнение теплопроводности

Модель первого порядка, описывающую работу элемента защиты от ESD, можно получить, определив максимальную мощность, которая может выделяться в элементе без его повреждения. Это позволяет вычислить максимальный ток, проводимый данным элементом, который и определяет порог устойчивости защитного устройства к ESD. В ряде исследований в качестве граничного условия работы для такой модели использовалась температура плавления кремния (1412ºС) или, в случае применения алюминиевых контактов, температура эвтектики Al-Si (550ºС). Но так как точно вычислить локальную температуру устройства в момент теплового пробоя невозможно, то необходимо настраивать модель, используя экспериментальные данные.

Моделирование начинается с решения уравнения теплопроводности элемента заданной геометрии - параллелепипеда со сторонами a, b и c, которые являются соответственно шириной канала, эффективной длиной канала и глубиной залегания pn-перехода. Решение этого уравнения позволяет получить зависимость максимальной рассеиваемой мощности, при которой происходит отказ защитного элемента, от времени стресса [1,2]. Эта зависимость показана на рис. 2.

Рисунок 2. Зависимость рассеиваемой мощности, при которой происходит отказ защитного элемента P_f, от времени ESD-стресса (логарифмическая шкала)

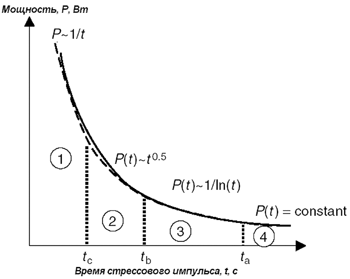
На графике можно выделить четыре характерные области.

Во время ESD-стресса тепловой фронт распространяется на расстояние L = (Dt)^½, что составляет порядка 10 мкм для импульса длительностью 1 мкс.

Это гораздо меньше, чем расстояние от защитного элемента до края кристалла. Можно считать, что тепло распространяется в бесконечном пространстве, то есть x и y стремятся к бесконечности, а температура в удаленных областях близка к температуре окружающей среды. Аналогичные оценки могут быть сделаны и для вертикальной оси. Таким образом, мы можем рассматривать источник тепла в полубесконечном пространстве - < x < , - < y < , z > 0.

Обычно область z < 0 покрывается окислом, и е╦ можно считать плохим проводником тепла. Поэтому границу z = 0 можно рассматривать как отражающую, и источник тепла по методу отображений переносится в область z < 0. Строго говоря, в направлении z < 0 структура не является теплоизоляционной из-за наличия поликремниевого затвора и металлизации, расположенной над pn-переходом в непосредственной близости от источника тепла, но оценки показывают, что их влияние невелико.

Сформулированная задача решается методом функции Грина [1]. Решение дает значения t_a, t_b, t_c и определяет зависимости мощности, при которой наступает отказ от времени стрессового импульса для соответствующих областей. Для очень малых времен, меньших t_c, рассеяния энергии не происходит, и для разрушения устройства требуется энергия (P_f╥t₂). На участке t_c < t < t_b критическая мощность пропорциональна 1/Цt, а затем на участке t_b < t < t_a становится пропорциональной 1/ln(t). Для времен, больших t_a, мощность отказа приближается к константе, которая означает, что рассеяние энергии стало равно е╦ генерации. При значениях 100, 1 и 0,1 мкм для а, b и c, соответственно, t_a, t_b и t_c принимают значения 10 мкс, 1 нс и 10 пс, соответственно. Таким образом, в случае ESD можно ожидать зависимость вида Р_f(t₂) ~ 1/ln(t) [1,2].

Результаты моделирования хорошо согласуются с экспериментами. Зависимость P_f от t выявляет порог отказа схемы в широком диапазоне времен стресса. С помощью этой зависимости можно классифицировать уровень защищенности от ESD в дополнение к стандартным методам, так как эту зависимость легко получить, обладая данными TLP-анализа (TransmI_ssion Line Pulsing, модель импульса линии передач).

Модель, использующая электрические и температурные выражения

Для точного описания поведения защитного элемента в режиме больших токов в предшествующей второму пробою области необходимо учитывать не только электрические, но и температурные зависимости параметров. В работах [1] и [2] приводятся зависимости плотности дырочного и электронного тока, коэффициента лавинной ионизации, подвижностей и электрических полей от температуры. На рис. 3 показаны результаты моделирования nМОП-транзистора, полученные на основе этих данных [1].

Рисунок 3. Ток температурной и лавинной генерации как функция температуры перехода (а); изменение напряжения стока от времени при постоянном токе инжекции (б)

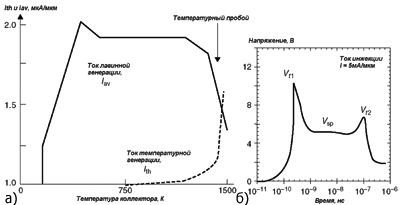
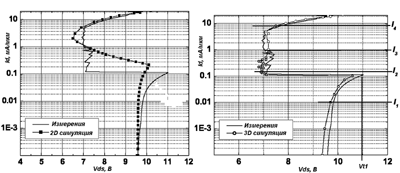
На рис. 3а показана зависимость токов лавинной и температурной генерации от температуры перехода. Второй пробой наступает, когда ток температурной генерации вырастает до значения, необходимого для работы паразитного биполярного транзистора. Ток лавинной генерации с этого момента начинает уменьшаться. Напряжение падает и становится нестабильным. На рис. 3б легко выделить все режимы работы транзистора при больших токах инжекции.

Приведенные аналитические модели являются полезным дополнением к стандартным методам определения порога устойчивости к ESD защитных структур и в совокупности с экспериментальными данными позволяют оптимизировать параметры схем защиты от ESD.

Компьютерное моделирование ESD в элементах защиты на основе физических моделей

Использование компьютерных программ моделирования работы ИС - важная часть разработки устройства. На данный момент существует довольно много двумерных (2D) программ моделирования, позволяющих описать двумерную структуру полупроводникового устройства, включая определение областей кремния и оксида, профили легирования, электроды, а также электрические модели устройства. Количественное соответствие результатов моделирования и экспериментальных данных достигается за счет подбора параметров модели. Но даже некалиброванные результаты моделирования могут быть использованы для качественного анализа работы устройства. Программы моделирования позволяют оценить плотность тока, электрическое поле, коэффициент лавинной ионизации, температуру и множество других факторов в любой точке ВАХ. Если откалиброванная программа моделирования точно рассчитывает физические процессы, протекающие в устройстве, она может быть использована для получения зависимости характеристик работы устройства от технологических и топологических параметров. Это особенно ценно, так как многие ESD тесты являются разрушающими. Такие программы позволяют описать поведение устройства при использовании HBM (Human Body Model, модель человеческого тела), MM (Machine Model, механическая модель), CDM (Charged DevI_ce Model, модель заряженного устройства), TLP-модели.

Выбор между 2D- и 3D-моделированием

Основной целью моделирования устройства, подверженного воздействию ESD, является получение ВАХ элемента и извлечение из не╦ критических параметров. При расчете токов, протекающих до защелкивания паразитного биполярного транзистора, температурными эффектами можно пренебречь, что позволяет получить эту часть ВАХ с помощью простого анализа по постоянному току (DC-анализ). Разогрев устройства после защелкивания зависит от величины протекающего тока и особенностей элемента. Моделирование этого участка наиболее сложно, так как увеличение температуры кристалла влияет на электрические параметры устройства и наоборот, параметры устройства определяют изменение температуры.

С помощью 2D-моделирования в работе [3] для элемента GGNMOST была получена ВАХ, изображенная на рис. 4. Для сравнения, на этом рисунке также изображена экспериментально полученная ВАХ для элемента с идентичными топологическими параметрами. Можно сделать вывод, что данный метод позволяет качественно промоделировать snapback-режим элемента. Вместе с тем, необходимо отметить, что изгиб перед включением паразитного биполярного транзистора рассчитанной ВАХ выражен более слабо, что приводит к более низкому напряжению защелкивания V_t1 по сравнению с экспериментом. Далее, в эксперименте элемент входит в низкоомный режим сразу же после защелкивания, в то время как моделирование предсказывает плавный переход в этот режим. Для I_D < 5 мА/мкм в эксперименте наблюдается вертикальный участок ВАХ, на котором дифференциальное сопротивление близко к нулю, а при моделировании резкого изменения наклона характеристики в точке I_D = 5 мА/мкм - не наблюдается. Вычисления показывают плавное поведение тока на всех участках. Причина несоответствия заключается в неоднородном защелкивании элемента в пределах его ширины, что можно описать только с помощью 3D-моделирования. В результате можно утверждать, что критические параметры, полученные с помощью 2D-моделирования, несколько отличаются от их реальных значений. Кроме напряжения защелкивания V_t1, также будет отличаться и величина напряжения низкоомного режима V_sb (в данном случае, на 0,75 В).

Рисунок 4. Сравнение ВАХ GGNMOST-транзистора, полученной с помощью 2D- и 3D-моделирования и ВАХ из эксперимента

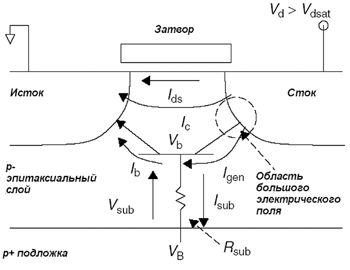
Рассмотрим подробнее причину неоднородности защелкивания элемента в пределах ширины канала. В реальных устройствах эффективная длина канала и толщина подзатворного окисла на краях канала будут отличаться от их значений в центральной области. Так как pn-переход вдоль канала имеет цилиндрическую форму, он становится сферическим в углах диффузионных областей. Более сильное искривление сферических областей по сравнению с цилиндрическими приводит к несколько большим электрическим полям в этих местах. Электрическое поле является фундаментальным параметром при описании полупроводникового элемента, и другие параметры, такие как коэффициент лавинного умножения, будут зависеть от трехмерной структуры элемента. Изменение напряжения пробоя от центра к углу элемента (то есть от цилиндрического перехода к сферическому) составляет около 0,8 В для 0,35-мкм технологии [3]. Есть и другие особенности реальных устройств, которые не могут быть отображены с помощью 2D-моделирования. Например, контакты к областям стока/истока находятся на определенном расстоянии от края области (заданном правилами топологического проектирования), что приводит к различию расстояний между контактом и затвором на краях областей стока/истока и в центре транзистора.

Для сокращения длительности расчетов 3D-модель GGNMOS-транзистора строится с помощью информации, полученной из 2D-моделирования. При этом двумерные профили легирования различных участков структуры переводятся в ряд аналитических функций. С помощью этих функций можно добиться очень точного воспроизведения профиля легирования. Затем 3D-генератор ячеек использует эти аналитические функции, чтобы собрать трехмерную структуру (рис. 5). Устройства, определенные таким образом, будут включать неоднородности вдоль периметра структуры (сферические/цилиндрические переходы), но погрешность, связанная с неидеальностью элемента, учтена не будет. Эта погрешность включает вариацию длины канала на протяжении ширины элемента, что в свою очередь влияет на распределение носителей под затвором.

Рисунок 5. Структура nМОП-транзистора с указанием токов в паразитном биполярном транзисторе

Для экономии времени вычисления дополнительно используют некоторые упрощения:

• в силу симметрии транзистора можно ограничиться вычислениями только для половины элемента;
• температурные граничные условия считают близкими к адиабатическим.

Используя такие допущения при 3D-моделировании, в работе [3] была получена ВАХ GGNMOST, изображенная на рис. 4. Результаты 3D-моделирования выявили следующие преимущества перед двумерным моделированием:

• полученная область snapback хорошо согласуется с экспериментом. Благодаря этому, полученные величины V_t11, I_t1 близки к реальным;
• резкий наклон ВАХ, имеющий место на графике тока высокой плотности, может быть воспроизведен с помощью 3D-моделирования практически точно. Напряжение низкоомного режима V_sb соответствует экспериментальным значениям.

Подводя итог, следует отметить, что работа устройств защиты от ESD является неоднородным процессом. По причине отмеченного изменения формы перехода напряжение защелкивания GGNMOST меньше всего на краях устройства, поэтому биполярный транзистор сначала включается именно здесь. Когда условие защелкивания элемента выполняется также и в середине элемента, стрессовый ток потечет и в эту область. Из-за определенных правил размещения контактов расстояние между контактом к стоку и затвором на крае диффузионной области будет отличаться от этой величины в центре, и сопротивление пути протекания тока через центр будет несколько меньше. Уровень тока, при котором будет достигнуто равномерное защелкивание элемента, зависит только от 2D-структуры устройства. Чем больше динамическое сопротивление, тем быстрее происходит растекание тока. Приведенные замечания справедливы для большинства известных технологий. В настоящее время ещ╦ не существует программ моделирования, учитывающих указанные неоднородности.

Из-за больших затрат времени программы 3D-моделирования в настоящее время не могут быть использованы в качестве стандартных приложений для расчета устройств защиты от ESD. Программы 2D-моделирования могут обеспечить необходимую точность вычислений для определения критических параметров. Однако не нужно забывать о проблемах, которые вс╦ же могут возникнуть при использовании 2D-программ моделирования. Измеряемая величина I_t1 всегда ниже, чем уровень тока, определяемый при помощи 2D-моделирования, так как паразитный биполярный транзистор в реальных условиях включается неравномерно. Также напряжение snapback-режима V_sb, определенное с помощью 2D-моделирования, будет всегда меньше либо равно измеренному в эксперименте. Это необходимо учитывать для грубой оценки опасности нежелательного защелкивания элемента во время нормальной работы, а также для оптимизации номинала нагрузочного резистора для выравнивания включения многоканальной структуры.

Проблема выбора граничных условий и оптимальной сетки расчета

Важным вопросом при моделировании является выбор области и подходящей сетки расчета, а также определение электрических и температурных граничных условий. С одной стороны, увеличивая область расчета, мы повышаем точность, но с другой стороны, это приводит к увеличению времени. Таблица содержит приблизительные данные по ESD-моделированию. Проблема выбора оптимальной сетки расчета также важна, поскольку разные области структуры обладают различной информативностью, например, более информативной будет область лавинной ионизации носителей на границе pn-перехода сток√подложка. Для оптимизации сетки существуют специальные математические методы.

Таблица. Время вычисления точек ВАХ для моделирования ESD в устройстве на рабочей станции с процессором 500 МГц

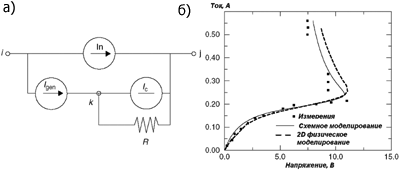
Моделирование элементов защиты от ESD на схемном уровне

Описание работы защитных устройств на схемном уровне позволяет оптимизировать работу элемента, не прибегая к дорогостоящим методам, требующим создания готовых изделий. Существующие программы аналогового моделирования, такие как SPI_cE, могут быть использованы для разработки и усовершенствования современных схем защиты от ESD. Далее будет рассмотрено аналоговое моделирование ряда наиболее важных элементов защитной схемы, которое может быть применено в аналогичных SPI_cE-программах. Соответствующие модели должны описывать работу схемы в режиме лавинного пробоя и режиме больших токов, так как именно эти режимы характерны для работы устройств под воздействием ESD. Модели также должны учитывать влияние топологии на сопротивление подложки, и в свою очередь, на работу устройства. Необходимо, чтобы параметры модели легко экстрагировались с помощью несложных вычислений.

Моделирование nМОП-транзистора

Большинство существующих программ аналогового моделирования не позволяют описать работу полевого транзистора в режиме больших токов, в то время как анализ схем защиты от ESD на МОП-транзисторах и объединение схем защиты с внутренней логикой предполагает точное описание работы схемы при воздействии ESD. Поэтому необходимо задать уравнения работы транзистора в соответствующих режимах.

Моделирование nМОП-транзистора должно включать в себя описание работы паразитного биполярного транзистора. Стандартные программы аналогового моделирования используют уравнения биполярных моделей, например, модели Гуммеля-Пуна, охватывающие нормальные режимы работы схем. Эти модели содержат ряд параметров, которые вычисляются исходя из информации, полученной при измерениях в нормальных условиях работы. Области ВАХ nМОП-транзистора схематично показаны на рис. 1. Крутая и пологая области работы полевого транзистора задаются стандартными уравнениями. Этими уравнениями нельзя описать область лавинного пробоя и низкоомную область, которые следуют за пологой областью. Плотности тока во время ESD обычно гораздо выше, чем при стандартных условиях работы nМОП-транзистора. Именно этим участком ВАХ описывается работа элемента во время ESD.

На рис. 5 показана структура nМОП-транзистора с обозначением токов во время стресса. Лавинная генерация носителей в области большого электрического поля в районе стока приводит к значительному дырочному току подложки I_sub. Падение напряжения на сопротивлении подложки Rsub, обеспечиваемое этим током, увеличивает локальный потенциал подложки Vsub и открывает тем самым переход исток√подложка. Электроны, инжектированные истоком в подложку, собираются стоком. Таким образом, формируется паразитный биполярный npn-транзистор, в котором эмиттером является исток, базой - подложка, а коллектором - сток. Эффективность этого транзистора определяется эффективностью эмиттера и коэффициентом переноса, который зависит от эффективной длины канала.

Для описания поведения паразитного биполярного транзистора в такой структуре может быть использована модель Гуммеля-Пуна, дополненная рядом параметров. Это увеличивает число необходимых измерений и усложняет программы моделирования. Всю необходимую информацию можно получить, зная ВАХ nМОП-транзистора в режиме больших токов, включая токи подложки, стока и истока. Чтобы модель МОП-транзистора можно было применить при разработке схем защиты от ESD, она должна соответствовать следующим требованиям:

• обеспечивать описание работы паразитного биполярного транзистора совместно с работой МОП-транзистора;
• включать сопротивления подложки и встроенных диодов для учета эффектов режима больших токов;
• включать, если возможно, небольшое число параметров, которые легко экстрагировать;
• уравнения модели должны быть достаточно простыми, хорошо согласовываться с экспериментом и не должны ухудшать точность и скорость работы программы моделирования;
• модель должна учитывать влияние топологии на работу устройства.

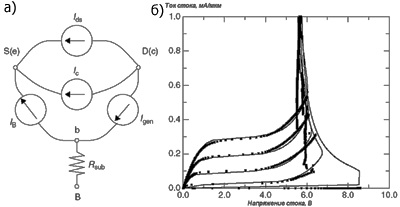
В работе [1] приводится расчет соответствующих уравнений модели:

где V_dch - напряжение насыщения сток√исток; V_gs - напряжение затвор√исток; V_t1h - пороговое напряжение; a, g - константы; M - фактор умножения лавинного пробоя; A_i, B_i - корректирующие параметры; V_bs - напряжение сток√исток; I_c - ток коллектора биполярного транзистора; b - коэффициент усиления биполярного транзистора; Q_b - учет эффекта деградации b в режиме больших токов; I_s - тепловой ток; V_bs, V_bd - напряжения база√исток, база√сток; V_t1 - температурный потенциал; I_b - ток базы; I_kf - ток, при котором деградация b становится значительной.

Эквивалентная схема паразитного биполярного транзистора представлена на рис. 6а.

Рисунок 6. Эквивалентная схема биполярного транзистора c источниками тока, необходимыми для описания режима snapback (а); сравнение данных эксперимента (точки) и результатов моделирования (сплошные линии) для nМОП-транзистора (б)

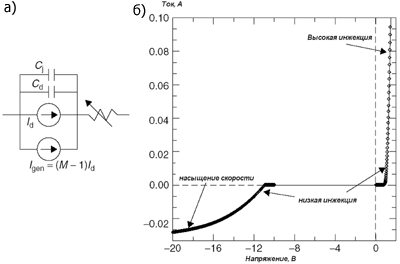
Также необходимо привести выражения, описывающие режим отсечки транзистора:

Сравнение данных эксперимента и результатов моделирования для nМОП-транзистора приведено на 6б. Важно отметить, что по сравнению с nМОП-транзистором, pМОП-транзистор не имеет snapback-режима при воздействии стресса. Это объясняется низкой подвижностью дырок и низким b у латерального pnp-транзистора.

Следующим важным моментом является моделирование сопротивления подложки. Сопротивление открытых диодов в субмикронных технологиях обычно составляет 5 Ом на мкм ширины элемента, в то время как в закрытом состоянии оно может быть в 10√100 раз больше. Для описания работы nМОП-транзистора в режиме больших токов необходимо точно моделировать это сопротивление. Учет необходимых эффектов приводится в расчетах работы [1].

Одним из важных аспектов работы nМОП-транзистора во время ESD является время его включения. Оно определяется временем пролета базы _ве паразитного биполярного транзистора. При длине канала менее 1 мкм время включения биполярного транзистора составляет менее 250 пс, в то время как время роста ESD-стресса по модели HBM и по модели MM составляет более 1 нс. В этом случае время включения паразитного биполярного транзистора можно не принимать во внимание. Электростатический разряд по модели CDM происходит очень быстро, в данном случае время роста импульса может быть меньше 250 пс. Чтобы учесть _ве, надо добавить эффективную диффузионную емкость между базой и эмиттером C_be и эффективную диффузионную емкость между базой и коллектором C_bc, которые будут функциями _ве и заряда базы:

где µ_eff - эффективная подвижность электронов; n_be - константа; L - длина канала; V_be - напряжение база√эмиттер.

Для C_bc можно записать аналогичное выражение.

Моделирование диффузионных резисторов

Диффузионные резисторы являются одними из наиболее важных элементов схем защиты от ESD. Они используются для развязки основной и вспомогательной схем защиты во входных и выходных защитных схемах. Неправильное моделирование их работы может привести к значительному ухудшению характеристик защитной схемы. Используя эффекты скорости насыщения при больших токах, такой резистор может обладать очень низким сопротивлением при нормальных условиях работы и достаточно большим, когда устройство подвержено ESD. Эквивалентная схема диффузионного резистора приводится на рис. 7а.

Рисунок 7. Эквивалентная схема диффузионного резистора, учитывающая эффекты скорости насыщения и лавинного пробоя (а); ВАХ диффузионного резистора на n-кармане с током насыщения около 200 мА (б)

Для учета эффектов режима больших токов необходимо усовершенствовать стандартную модель диффузионного резистора, добавив источники тока, дающие основной вклад именно в этом режиме. Работа источников тока задается следующими уравнениями:

где I_n - электронный ток; I_gen - ток носителей, генерированных лавинным пробоем; I_c - дополнительный ток лавинной ионизации, является частью тока генерации; - параметр, определяющий область, в которой дрейфовый ток I_n вызывает генерацию дополнительных носителей; µn, µp - подвижности электронов и дырок, соответственно; V_ij - напряжение на резисторе; L - эффективная длина резистора; X_j - эффективная глубина залегания pn-перехода; W - эффективная ширина резистора; n, p - концентрации дырок и электронов, соответственно.

На рис. 7б показано сравнение результатов эксперимента: 2D физического моделирования и аналогового моделирования.

Моделирование защитных диодов

Как уже отмечалось, для описания работы устройства, подверженного ESD, необходимо точное моделирование работы диодов в режиме больших токов. Работа открытых и закрытых диодов определяет эффективное сопротивление подложки. Эквивалентная схема защитного диода приведена на рис. 8а. Рис. 8б показывает ВАХ диода, полученную с помощью этой модели.

Рисунок 8. Эквивалентная схема защитного диода, включающая ток диода I_D, ток лавинной ионизации I_gen, емкость pn-перехода C_j и диффузионную емкость С_D. Номинал резистора изменяется в зависимости от направления тока (а); ВАХ p+/n+ диода (б)

Заключение

Физическое моделирование с учетом температурных эффектов очень полезно для анализа результатов эксперимента. Аналитические модели могут быть использованы для оценки влияния технологических и топологических параметров на работу защитных структур. Кроме того, физическое моделирование позволяет лучше понять природу эффектов, возникающих в ИС при ESD. Это помогает усовершенствовать существующие схемы защиты от ESD и создавать новые. Учитывая пользу физического моделирования, можно отметить, что оно является желательным этапом разработки схем защиты.

Важным моментом в данном случае является выбор между 2D и 3D физическим моделированием, так как это обеспечивает различный порядок точности модели. 2D-моделирование относительно просто и может обеспечить достаточно высокий порядок точности, но значения V_t1 и V_sb получаются несколько ниже, чем на самом деле. 3D-модель позволяет более точно описать ESD-стресс, учитывая неоднородность защелкивания элемента, связанную с различной формой pn-перехода на краях и вдоль диффузионной области, а также изменение расстояния между контактами к стоку/истоку и затвором. Используя данный подход 3D-моделирования [3], были достигнуты следующие результаты: полученная область snapback очень хорошо согласуется с экспериментом. Благодаря этому полученные величины V_t1, I_t1 близки к реальным. Напряжение низкоомного режима V_sb хорошо согласуется с экспериментальными значениями.

Из-за огромного времени расчета 3D-программы моделирования на данный момент не могут быть использованы в качестве стандартных приложений для моделирования устройств защиты от ESD. Программы 2D-моделирования могут обеспечить необходимую точность вычислений для определения критических параметров. Однако нужно помнить о проблемах, которые возникают при их использовании. Измеряемая величина I_t1 всегда ниже, чем уровень тока, определяемый с помощью 2D-моделирования. Напряжение snapback-режима V_sb, определенное с помощью 2D-моделирования, будет всегда меньше либо равно измеренному в эксперименте.

Вторая часть статьи описывает основы моделирования структур защиты от ESD на схемном уровне. Наибольшее внимание уделено моделированию работы МОП-транзисторов в режиме больших токов, важной частью которого является описание работы паразитного биполярного транзистора. Как было отмечено, модель Гуммеля-Пуна должна быть дополнена уравнениями, учитывающими лавинный пробой pn-переходов. Такое усовершенствование модели Гуммеля-Пуна дает возможность оптимизировать схемы защиты от ESD, не прибегая к реализации изделия в кремнии и дорогостоящему разрушающему тестированию до окончания разработки. Была также рассмотрена модель диффузионного резистора, учитывающая эффекты насыщения тока и лавинного пробоя, и модель защитного диода. Оба рассмотренных подхода к моделированию работы защитного устройства на физическом и схемном уровне имеют свои преимущества и заслуживают внимания разработчиков.

Литература

1. Ajith Amerasekera, Charvaka Duvvury. ESD in Silicon Integrated Circuits. 2nd Edition, 2002.
2. Stephen G. Beebe. CHARACTERIZATION, MODELING, AND DESIGN OF ESD PROTECTION CIRCUITS. Advanced Micro Devices. Саннивэйл, Калифорния, 1998.
3. Kai Esmark. Device Simulation of ESD Protection Elements. dissertation for the degree of Doctor of Technical Sciences, 2001.