Необходимые сведения - Статистика электронов и дырок в полупроводникахТвердотельная электроника. Учебное пособие.
1.3. Статистика электронов и дырок в полупроводниках
Равновесные процессы - процессы, происходящие в телах, которые не подвергаются внешним воздействиям. В состоянии термодинамического равновесия для данного образца кристалла при заданной температуре существует определенное распределение электронов и дырок по энергиям, а также значения их концентраций. Вычисление концентраций основных и неосновных носителей заряда составляет главную задачу статистики электронов и дырок в кристаллах.
Рассматриваемая задача распадается на две части: чисто квантово-механическую - нахождение числа возможных квантовых состояний электронов и статистическую - определение фактического распределения электронов по этим квантовым состояниям при термодинамическом равновесии.
1.3.1. Распределение квантовых состояний в зонах
Стационарные состояния электрона в идеальном кристалле характеризуются квазиимпульсом р. Запишем принцип неоднородностей Гейзенберга для квазиимпульсов dpx, dpy и dpz:
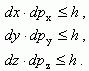(1.1)Перемножим соответственно левые и правые части этих соотношений. Получим
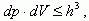(1.2)где dp = dpx·dpy·dpz и dV = dx·dy·dz, то есть dp - это некоторый объем в пространстве квазиимпульсов px, py, pz, то есть внутри зоны Бриллюэна, а dV - некоторый объем внутри полупроводника. При этом объем dV - не обязательно бесконечно малая величина. Он может быть и конечным. Для расчета концентраций носителей заряда (то есть числа носителей в единице объема полупроводника) выделим внутри кристалла единичный объем dV = 1 см3. Тогда из (1.2) получим dp ≤ h3. То есть внутри объема dp = h3 в зоне Бриллюэна может иметь место только одно квантовое состояние, которое как бы размыто по всему этому объему. Итак, h3 - это объем одной "квартирки" в зоне Бриллюэна, в которую можно поместить только два электрона с разными спинами, и не более. Поэтому число квантовых состояний, соответствующее элементу объема dp в зоне Бриллюэна и рассчитанное на единицу объема кристалла, равно dp/h3 - то есть числу "квартирок" в объеме dp. При заполнении зоны проводимости электронами заполняются вначале самые нижние уровни. Зона проводимости - одномерная относительно энергии (рис. 1.3а). Зона Бриллюэна - трехмерная (px, py, pz) (рис. 1.3б). Заполнение зоны Бриллюэна начинается с самых малых значений квазиимпульса p. Поэтому в качестве dp надо выбрать элемент объема, заключенный между двумя очень близкими изоэнергетическими поверхностями (см. рис. 1.3б). Внутри этого тонкого шарового слоя радиусом p и толщиной dp число квантовых состояний будет равно:
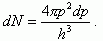(1.3)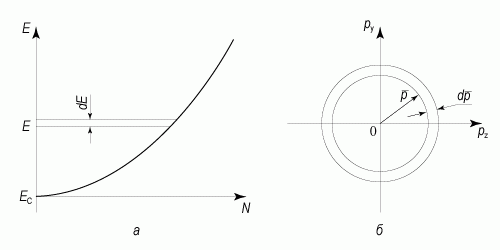
Рис. 1.3. Диаграмма для расчета плотности квантовых состояний:
а - распределение электронов по энергии в зоне проводимости;
б - зона Бриллюэна для расчета плотности состояний
Определим число квантовых состояний в зоне проводимости в узком интервале энергий от Е до Е+dЕ, рассчитанное на единицу объема кристалла. Его можно представить в виде N(E)dE, где N(E) есть плотность состояний.
Вблизи дна зоны проводимости для случая изотропного параболического закона дисперсии энергия электрона
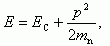(1.4)где ЕC - энергия, соответствующая дну зоны проводимости. Для удобства эффективную массу электрона mn будем писать без звездочки. Из (1.4) получим dE = p·dp/mn, то есть dp = mndE/p и p2 = 2mn(E-Ec). Подставляем в (1.3), имеем
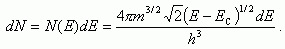(1.5)Отсюда
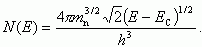(1.6)Аналогичная формула получается и для валентной зоны, но только вместо (Е - ЕC) напишем (ЕV - Е), а вместо mn - эффективную массу дырки mp.
Как видно из (1.6), плотность квантовых состояний возрастает по мере удаления от дна зоны проводимости.
1.3.2. Концентрация носителей заряда и положение уровня Ферми
Электроны, как частицы, обладающие полуцелым спином, подчиняются статистике Ферми-Дирака. Вероятность того, что электрон будет находиться в квантовом состоянии с энергией Е, выражается функцией Ферми-Дирака:
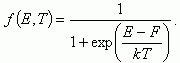(1.7)Здесь F - электрохимический потенциал, или уровень Ферми. Из (1.7) видно, что уровень Ферми можно определить как энергию такого квантового состояния, вероятность заполнения которого равна 1/2.
Вид функции Ферми-Дирака схематически показан на рисунке 1.4. При Т = 0 она имеет вид разрывной функции. Для E < F она равна 1, а значит, все квантовые состояния при E < F заполнены электронами. Для E > F функция f = 0 и соответствующие квантовые состояния совершенно не заполнены. При Т > 0 функция Ферми изображается непрерывной кривой и в узкой области энергий, порядка нескольких kT, в окрестности точки E = F быстро изменяется от 1 до 0. Размытие функции Ферми тем больше, чем выше температура.
Вычисление различных статистических величин значительно упрощается, если уровень Ферми F лежит в запрещенной зоне энергий и удален от края зоны ЕC хотя бы на 2kT (в некоторых учебниках пишут ЕC - Е > kT). Тогда в распределении (1.7) единицей в знаменателе можно пренебречь и оно переходит в распределение Максвелла - Больцмана классической статистики. Это случай невырожденного полупроводника:
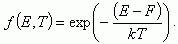(1.8)Концентрация электронов в зоне проводимости равна:
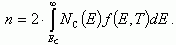(1.9)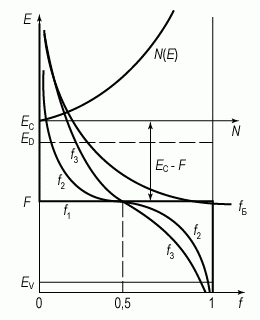
Рис. 1.4. Функция распределения плотности состояний в зоне проводимости N(E), функции Ферми-Дирака f и Больцмана fБ
Отметим, что в качестве верхнего предела в написанном интеграле мы должны были бы взять энергию верхнего края зоны проводимости. Но, так как функция f для энергий E > F экспоненциально быстро убывает с увеличением E, то замена верхнего предела на бесконечность не меняет значения интеграла. Подставляем в (1.9) выражения (1.6) и (1.8). Расчет интеграла несложен. Получим
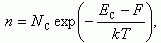(1.10)где
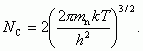(1.11)Величина NC получила название эффективной плотности состояний в зоне проводимости.
В случае невырожденного полупроводника, когда уровень Ферми лежит выше потолка валентной зоны хотя бы на 2kT, то есть F - EC > 2kT (в некоторых учебниках пишут F - EC > kT), функция Ферми-Дирака для дырок fp имеет вид
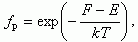(1.12)а концентрация дырок в валентной зоне
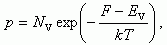(1.13)где EV - энергия, соответствующая потолку валентной зоны, а NV рассчитывается по уравнению (1.11), если вместо mn взять эффективную массу дырки mp. Величина NV - эффективная плотность состояний в валентной зоне.
Отметим, что в (1.9) перед интегралом появился множитель 2, что связано с тем, что на каждом уровне энергии могут находиться два электрона с противоположными спинами (принцип Паули).
Для расчета n и p по уравнениям (1.10) и (1.13) необходимо знать положение уровня Ферми F. Однако произведение концентраций электронов и дырок для невырожденного полупроводника не зависит от уровня Ферми, хотя зависит от температуры:
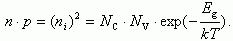(1.14)Это уравнение используется для расчета p при известном n или, наоборот, для расчета n при известном p. Величина ni при некоторых температурах для конкретных полупроводников приводится в справочниках.
Copyright © 2003-2008 Авторы
|
Gonzogerd пишет... Какое значение для человека имеет вода, объяснять никому не надо. Без нее, просто невозможно существование ни человека, ни животных, поскольку, все процессы, http://poverka16.ru/>поверка счетчиков водыпротекающие в организме, проходят в растворенном виде. Но вода нужна не только для питья и приготовления пищи, без нее не обходится и хозяйственная деятельность, надо же постирать, влажную уборку провести, в конце концов.
02/06/2016 03:42:03 |
|
Dimplesget68 пишет... Ведь видимые трещины в фундаменте или перекосившиеся стены не позволят даже надеяться на компенсацию расходов. Что уж говорить о прибыли. http://variant123.ru/thorough_repair/>ремонт помещений сочи Так что прежде, чем принимать решение купить участок, стоит подумать над тем, чтобы посоветоваться хотя бы с друзьями или близкими, которые уже прошли через подобные испытания. 16/06/2016 22:45:35 |
|
Fifoweb49 пишет...
20/06/2016 14:01:20 |
|
Yumbairk пишет... Ремонтные работы можно разделить на текущие, косметические или капитальные. Во время текущего ремонта устраняют мелкие дефекты помещения. Подклеивают http://remont-nw.ru/uteplenie-balkona-i-lodzhij>утепление балконов и лоджий с умом и только по согласованию с городскими службами, так как разлом несущей стены приведет к разрушению всего дома. При капитальном ремонте нельзя: Сносить 02/07/2016 02:02:39 |
|
Howlamaira пишет... Как обычно, предмет, который необходимо отыскать, является заданием, приводящим к победе. Слово квест с английским происхождением означает поиск. http://exit39.ru/>квесты в калининграде цена вероятно, позитивным настроением охранника, выйти из помещения. 06/07/2016 21:52:41 |
|
LarryCidly пишет... Приобрести сироп Mangoosteen можно на веб-сайте http://mangjoo77.mangoosteen.com
24/07/2017 19:28:00 |
|
LarryCidly пишет... Приобрести сироп Mangoosteen можно на веб-сайте http://mangjoo77.mangoosteen.com
25/07/2017 17:06:05 |
|
LarryCidly пишет... Хотим предложить вам потрясающее средство для похудения Mangoosteen. С ним можно избавиться от 15 кг за 14 дней.
28/07/2017 17:23:12 |
|
DonaldRof пишет... http://super-steamer.mega-shop.ru
06/09/2018 19:00:20 |
|
FikrocsHap пишет... Отличную обувь всегда тяжело найти. Связано это изначально с тем, что модные кроссовки дорого стоят, а подобрать что-то модное по низкой цене всегда трудно. Если вы не уверены, в каком магазине купить кроссовки, рекомендуем рассмотреть шанс покупки кроссовок в интернет-магазинах.
19/12/2018 07:30:07 |
| Ваш комментарий к статье | ||||
