6.11. Вольт-амперная характеристика МДП-транзистора в области сильной и слабой инверсии

После того, как из решения уравнения Пуассона получена зависимость заряда свободных носителей Q_n(ψ_s, φ_c) как функция поверхностного потенциала и квазиуровня Ферми, а из уравнения непрерывности - связь между поверхностным потенциалом и квазиуровнем Ферми, можно вернуться к выражению для тока канала (6.43) и получить в явном виде вольт-амперную характеристику МДП-транзистора.

В области сильной инверсии из (6.43), (6.67) и (6.69) следует, что

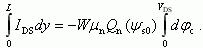   (6.72)

После интегрирования и учета того, что для области сильной инверсии в уравнении непрерывности (6.65) в правой части доминирует последний член, получаем:

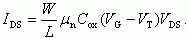   (6.73)

Отметим, что для области сильной инверсии, т.е. в приближении плавного канала, ВАХ МДП-транзистора в виде (6.73) совпадает с ВАХ, полученной нами ранее в простейшем случае в виде (6.10).

В области слабой инверсии из (6.44), (6.57) и (6.67) следует, что

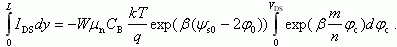   (6.74)

После интегрирования (6.74) и учета того, что уравнение непрерывности (6.58) дает для этого случая

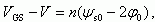   (6.75)

получаем:

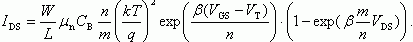   (6.76)

Соотношение (6.76) представляет собой вольт-амперную характеристику МДП-транзистора для области слабой инверсии. На рисунках 6.11, 6.12 приведены проходные и переходные характеристики транзистора в этой области. Обращает на себя внимание тот факт, что в области слабой инверсии зависимость тока стока I_DS от напряжения на затворе V_GS - экспоненциальная функция, причем экспоненциальный закон сохраняется на много порядков. Ток стока не зависит практически от напряжения на стоке, выходя на насыщение при напряжениях исток-сток V_DS порядка долей вольта. Напомним, что при слабом захвате (N_ss → 0) ток канала имеет диффузионный характер. Для случая, когда МДП-транзистор работает при напряжениях на затворе V_GS больше порогового напряжения V_T и напряжениях на стоке V_DS больше напряжения отсечки V_DS^*, т.е. в области насыщения тока стока, ситуация усложняется. Точка отсечки соответствует переходу от области сильной к области слабой инверсии. Слева к истоку от точки отсечки канал находится в области сильной инверсии, ток в канале дрейфовый, заряд свободных электронов постоянен вдоль канала. Справа к стоку от точки отсечки область канала находится в слабой инверсии, ток в канале диффузионный, заряд свободных электронов линейно изменяется вдоль инверсионного канала. На рисунке 6.10 видно, что область перехода от сильной к слабой инверсии на зависимости ψ_s = φ_c выражается перегибом, что соответствует изменению соотношения между дрейфовой и диффузионными составляющими тока канала. Таким образом, в области отсечки ток в канале вблизи истока в основном дрейфовый, при приближении к стоку в области отсечки резко возрастет диффузионная составляющая, которая при нулевом захвате равна у стока полному току канала.

Предыдущий анализ позволяет получить распределение вдоль инверсионного канала квазиуровня Ферми φ_c, его градиента dφ_c/dy и заряда свободных носителей Q_n(у). За основу возьмем выражение для полного тока в канале в виде (6.44). Будем считать, что подвижность μ_n не меняется вдоль инверсионного канала. Из условия непрерывности тока следует, что произведение

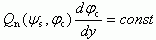   (6.77)

должно оставаться величиной, постоянной вдоль инверсионного канала. Заметим, что при больших величинах напряжения исток-сток V_DS допущение о постоянстве подвижности μ_n = const может не выполняться. Физически зависимость подвижности μ_n от положения вдоль канала может быть обусловлена ее зависимостью от концентрации свободных носителей. Поэтому в дальнейшем будем считать напряжение исток-сток V_DS малым, когда μ_n = const.

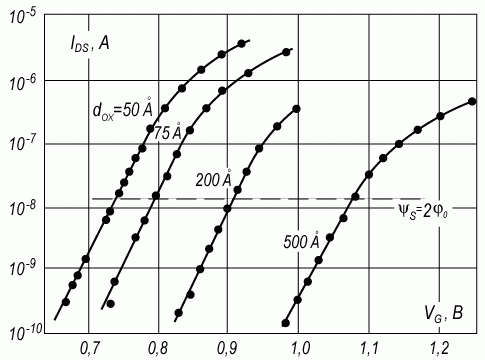
Рис. 6.11. Зависимость тока стока I_DS от напряжения на затворе V_G в предпороговой области для МДП-транзисторов с разной толщиной подзатворного диэлектрика. Стрелками на кривых показаны области перехода от экспоненциальной к более плавной зависимости тока стока I_DS от напряжения на затворе. Напряжение исток-сток V_DS = 0,025 В

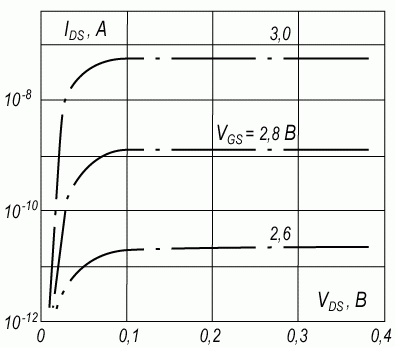
Рис. 6.12. Зависимость тока стока I_DS от напряжения на стоке V_DS в области слабой инверсии при различных предпороговых значениях напряжения на затворе V_G. V_T = 2,95 В

Для области слабой и сильной инверсий соотношения (6.57), (6.67), (6.58), (6.69) дают соответственно:

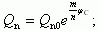   (6.78)

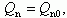   (6.79)

где Q_n0 - заряд электронов в канале при φ_c = 0 (или вблизи истока, или при равновесных условиях).

Проведем интегрирование уравнения (6.77) с учетом (6.78) и (6.79) и с граничными условиями:

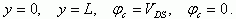
Предполагается, что длина канала L много больше области изменения легирующей концентрации вблизи стока и истока.

Получаем выражения для распределения квазиуровня Ферми вдоль канала в области слабой инверсии:

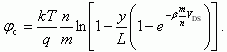   (6.80)

Для градиента квазиуровня получаем после дифференцирования (6.80):

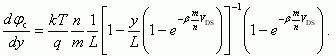   (6.81)

Поскольку вдоль инверсионного канала произведение (6.77) остается постоянным, то, следовательно, заряд свободных электронов Q_n линейно спадает вдоль канала, как вытекает из (6.81):

   (6.82)

Ha рисунке 6.13а, б приведены величины квазиуровня и его градиента ∂φ_c/∂y как функция координаты вдоль канала у в области слабой инверсии.

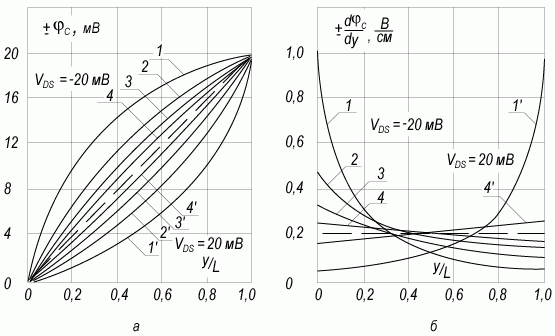
Рис. 6.13. Распределение потенциала вдоль инверсионного канала
а) распределение квазиуровня Ферми φ_c; б) распределение градиента квазиуровня Ферми ∂φ_c/∂y вдоль инверсионного канала: 1,1' - m/n =1; 2,2' - m/n = 0,5; T = 80 K, 3,3' - m/n = 1; 4,4' - m/n = 0,5; T = 290 K. Пунктирная линия соответствует линейному распределению квазиуровня Ферми φ_c вдоль канала

Для области сильной инверсии (6.77) с учетом (6.79) и (6.80) дает:

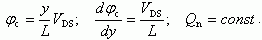   (6.83)

Следовательно, в области сильной инверсии квазиуровень Ферми φ_c линейно меняется вдоль канала, заряд электронов постоянен в каждой точке канала. Отметим, что соотношения (6.58), (6.69), являющиеся основой (6.79), справедливы в области сильной инверсии, когда β(ψ_s - 2φ₀ - φ_c) > 7. Численный расчет уравнения (6.77) для всего реально изменяющегося диапазона поверхностных избытков Γ_n приведен на рисунке 6.14. Из рисунка 6.14 следует, что в области избытков Γ_n << 10⁹ см^-2 справедливы соотношения (6.80 - 6.82), а в области Γ_n > 10¹² см^-2 - соотношения (6.83). В промежуточной области необходим численный расчет.

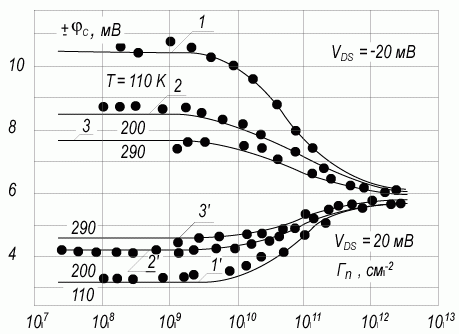
Рис. 6.14. Зависимость квазиуровня Ферми φ_c в точке канала y/L = 0,3 в зависимости от избытка электронов Γ_n при равных температурах Т и напряжениях V_DS. Точки - эксперимент, сплошная линия - расчет