Барьеры Шоттки и pn-переходы - Образование и зонная диаграмма p-n переходаТвердотельная электроника. Учебное пособие.
2.10. Образование и зонная диаграмма p-n перехода
Электронно-дырочным, или p-n переходом, называют контакт двух полупроводников одного вида с различными типами проводимости (электронным и дырочным).
Классическим примером p-n перехода являются: n-Si - p-Si, n-Ge - p-Ge.
Рассмотрим контакт двух полупроводников n- и p-типа. Величина работы выхода Ф определяется расстоянием от уровня Ферми до уровня вакуума. Термодинамическая работа выхода в полупроводнике p-типа Фp всегда больше, чем термодинамическая работа выхода Фn в полупроводнике n-типа. Из соотношений (2.13) и (2.14) следует, что
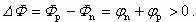
При контакте полупроводников n- и p-типов вследствие различного значения токов термоэлектронной эмиссии (из-за разных значений работы выхода) поток электронов из полупроводника n-типа в полупроводник p типа будет больше. Электроны из полупроводника n-типа будут при переходе в полупроводник p-типа рекомбинировать с дырками. Вследствие несбалансированности токов в полупроводнике n-типа возникнет избыточный положительный заряд, а в полупроводнике p-типа - отрицательный. Положительный заряд обусловлен ионизованными донорами, отрицательный заряд - ионизованными акцепторами. Вследствие эффекта поля произойдет изгиб энергетических зон в полупроводниках n- и p-типов, причем в полупроводнике p-типа на поверхности термодинамическая работа выхода будет уменьшаться, а в полупроводнике n-типа на поверхности термодинамическая работа выхода будет увеличиваться. Условию термодинамического равновесия соответствуют равные значения токов термоэлектронной эмиссии с поверхности полупроводников p- и n-типов, а следовательно, и равные значения термодинамической работы выхода.
На рисунке 2.8 приведены зонные диаграммы, иллюстрирующие этапы формирования электронно-дырочного перехода.
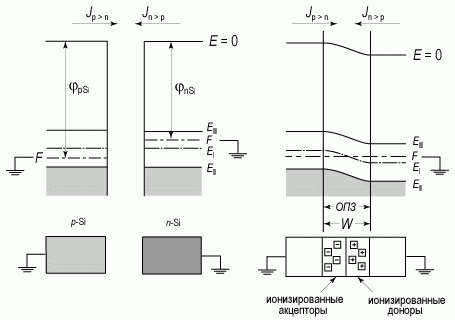
Рис. 2.8. Схема, иллюстрирующая образование p-n перехода
Граница областей донорной и акцепторной примеси в полупроводнике получила название металлургического p-n перехода. Границу, где уровень Ферми пересекает середину запрещенной зоны, называют физическим p-n переходом.
2.10.1. Распределение свободных носителей в p-n переходе
Рассмотрим несимметричный p-n переход, будем считать, что концентрация акцепторов больше, чем концентрация доноров NA > ND; в этом случае для объемного положения уровня Ферми получаем φn < φp. В условиях равновесия (VG = 0) высота потенциального барьера p-n перехода будет
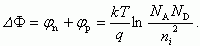(2.42)Рассмотрим распределение свободных носителей - электронов и дырок в области пространственного заряда p-n перехода.
Для квазинейтрального объема полупроводников
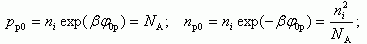
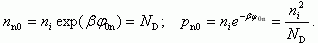(2.43)Для области пространственного заряда эти соотношения трансформируются таким образом, что φ0p и φ0n становятся зависимыми от координаты x, то есть φ0p(x) и φ0n(x). Следовательно, и концентрации электронов и дырок в области пространственного заряда тоже зависит от координаты pp(x), np(x), nn(x), pn(x).
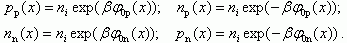(2.44)Рассмотрим, как меняется концентрация основных и неосновных носителей в p - области ОПЗ. В p - n переходе величина φp квазилинейно уменьшается, поэтому концентрация дырок pp будет экспоненциально убывать. Уровень Ферми совпадает с серединой запрещенной зоны у физического p - n перехода (φp = 0), в этой точке концентрация дырок становится равной собственной концентрации pp = ni.
Для электронов аналогично получаем, что величина концентрации электронов np(x) возрастает экспоненциально и также равна собственной концентрации в области физического p-n перехода.
Аналогично меняется концентрация основных nn(x) и неосновных pn(x) носителей в ОПЗ полупроводника n-типа.
На рисунке 2.9 показано распределение концентрации носителей в несимметричном p-n переходе в логарифмическом масштабе и схема p-n перехода.
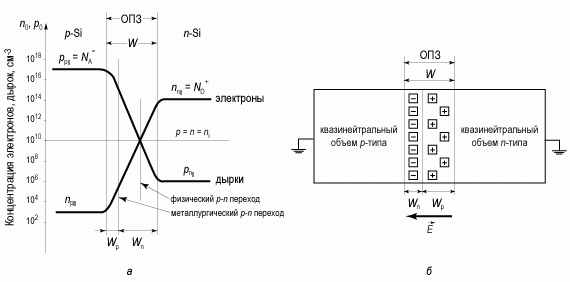
Рис. 2.9. p-n переход в равновесных условиях:
а) распределение равновесных носителей;
б) диаграмма, иллюстрирующая распределение доноров и акцепторов
Таким образом, из приведенного рисунка следует, что в несимметричных p-n переходах физические и металлургические p-n переходы пространственно не совпадают. Распределение концентрации основных и неосновных носителей симметрично относительно линии, соответствующей собственной концентрации ni.
2.10.3 Поле и потенциал в p-n переходе
Связь электрического поля и потенциала в p-n переходе описывается уравнением Пуассона. В одномерном приближении это уравнение имеет вид:
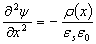(2.45)где ψ(x) - зависимость потенциала от координаты, ρ(x) - плотность объемного заряда, εs - диэлектрическая проницаемость полупроводника, ε0 - диэлектрическая постоянная.
Для рассмотрения этого уравнения выберем начало координат в области металлургического p-n перехода. При этом донорный полупроводник будет находиться в области x > 0 (в дальнейшем обозначим цифрой I), а акцепторный в области x < 0 (в дальнейшем обозначим цифрой II).Заряд в области пространственного заряда p-n перехода для полупроводника n-типа обусловлен зарядом ионизованных доноров с плотностью ND+, для полупроводника p-типа зарядом ионизованных акцепторов с плотностью NA+. Поэтому для области I, ρ(x) = qND+ для области II ρ(x) = qNA+. Будем решать уравнение Пуассона отдельно для областей I и II. После интегрирования уравнения Пуассона получаем для области I:
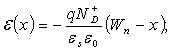(2.46)Для области II:
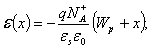(2.47)Знак "минус" в выражениях (2.46) - (2.47) указывает, что направление электрического поля противоположно направлению оси x.
Из соотношения (2.34) следует, что электрическое поле Е максимально на металлургической границе p-n перехода (x = 0), линейно спадает по области пространственного заряда и равно нулю на границах ОПЗ - квазинейтральный объем полупроводника (x = Wn; x = Wp).
Максимальная величина электрического поля Emax будет равна
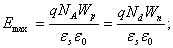(2.48)Для нахождения распределения потенциала (а следовательно и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.34) при следующих граничных условиях: x = W, ψ(W) = 0. Получаем:
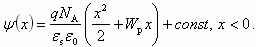(2.49)Используя граничные условия x = -Wp; ψ = Δφ0, находим константу интегрирования:
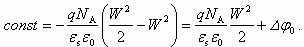
Подставляя полученные значения константы в соотношение (2.49), получаем для распределения потенциала ψ(x) в области x < 0.
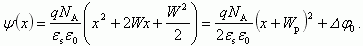
Проводя аналогичное интегрировнаие для области x > 0, получаем:
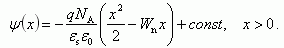(2.50)Используя граничные условия x = -Wn; ψ = 0; для константы интегрирования в этой области получаем:
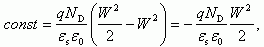
Подставляя полученные значения константы в соотношение (2.50), получаем для распределения потенциала ψ(x) в области x > 0:
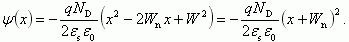(2.51)Таким образом, закон изменения потенциала ψ в p-области (отсчет идет от уровня в квазинейтральной области):
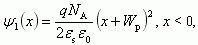
и наоборот, в n-области:
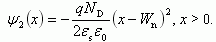
На рисунке 2.10 приведена диаграмма, иллюстрирующая распределение электрического поля и потенциала в p-n переходе, рассчитанная по соотношениям (2.46), (2.47), (2.50) и (2.51).
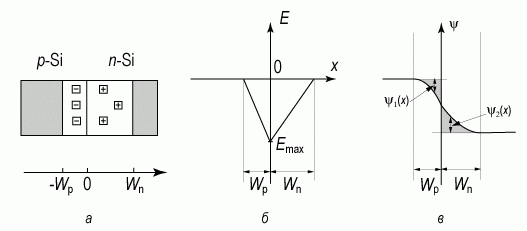
Рис. 2.10. Диаграмма, иллюстрирующая распределение электрического поля и потенциала в p-n переходе:
а) структура p-n перехода;
б) распределение электрического поля в ОПЗ;
в) распределение потенциала в ОПЗ
На металлургической границе p-n перехода при x = 0 значение потенциала ψ1 + ψ2 = Δφ0 = φn0 + φp0, или
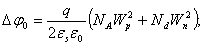(2.52)Согласно уравнению электронейтральности в замкнутых системах величины положительного и отрицательного заряда на единицу площади должны быть равны:
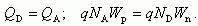
Следовательно,
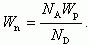(2.53)Подставляем выражение (2.45) в (2.46), получаем:
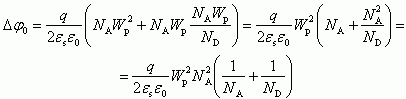
Несложные преобразования позволяют получить выражение для ширины обедненных областей Wp и Wn в p- и n-областях соответственно:
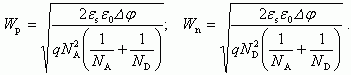(2.54)Из предыдущих формул легко видеть, что с ростом легирования p-области ширина p-n перехода Wp в акцепторной части полупроводника уменьшится.
Полная ширина p-n перехода W, равная W = Wp + Wn, будет:
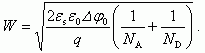(2.55)Для несимметричных p+-n переходов (концентрация акцепторов существенно больше концентрации доноров) из соотношений (2.47) и (2.48) следует, что ширина обедненной области в полупроводнике p-типа будет существенно меньше, чем ширина обедненной области в полупроводнике n-типа:
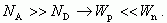
Таким образом, вся обедненная область p+-n перехода сосредоточена в области с низким значением легирующей концентрации W = Wn.
Copyright © 2003-2008 Авторы
| Ваш комментарий к статье | ||||
