2.5. Дебаевская длина экранирования

Количественной характеристикой эффекта поля, характеризующей глубину проникновения поля в полупроводник, является дебаевская длина экранирования. Рассмотрим случай, когда полупроводник внесен во внешнее слабое поле. Критерий слабого поля заключается в том, что возмущение потенциальной энергии невелико по сравнению с тепловой энергией, то есть величина поверхностного потенциала ψ_s будет меньше kT/q. Воспользуемся для нахождения распределения электростатического потенциала ψ_s в ОПЗ уравнением Пуассона, при этом будем считать, что ось z направлена перпендикулярно поверхности полупроводника:

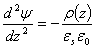   (2.18)

где ρ(z) - плотность заряда в ОПЗ,

ε_s - относительная диэлектрическая проницаемость полупроводника.

Заряд в ОПЗ состоит из заряда ионизованных доноров и заряда свободных электронов

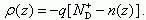   (2.19)

Величина N_D⁺ = n₀, а n(z) описывается соотношением (2.16). Поскольку в нашем случае βψ_s << 1, то

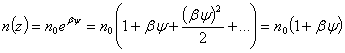   (2.20)

Тогда плотность объемного заряда

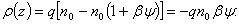   (2.21)

Подставляя значение ρ(z) из (2.21) в (2.18), получаем:

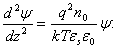   (2.22)

Введем характерную величину

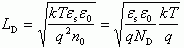   (2.23)

и назовем ее дебаевской длиной экранирования.

Тогда уравнение (2.22) придет к виду:

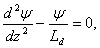   (2.24)

Решение дифференциального уравнения (2.24) имеет вид

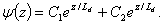   (2.25)

Используем граничные условия:
При z → ∞, ψ(z) → 0, получаем C₁ = 0,
При z = 0, получаем С₂ = ψ_s

Таким образом, при малом возмущении электростатический потенциал, а следовательно и электрическое поле, спадают по экспоненциальному закону вглубь полупроводника

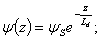
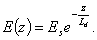   (2.26)

Известно, что если произвольная величина f(z) описывается законом

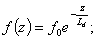   (2.27)

то среднее значение z, определяющее центроид функции f(z)

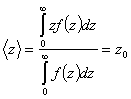   (2.28)

Таким образом, по физическому смыслу дебаевская длина экранирования L_D соответствует среднему расстоянию, на которое проникает электрическое поле в полупроводник при малых уровнях возмущения.