2.8. Распределение электрического поля и потенциала в барьере Шоттки

Рассмотрим более детально, как меняются электрическое поле и потенциал в области пространственного заряда контакта металл - полупроводник в виде барьера Шоттки. Для определенности будем рассматривать полупроводник n-типа. За знак приложенного напряжения будем считать знак напряжения приложенного к металлическому электроду, полупроводниковый электрод считаем заземленным.

Вне зависимости от полярности напряжение для барьерных структур все внешнее напряжение будет приложено к области пространственного заряда, поскольку в этой области концентрация свободных носителей существенно меньше, чем в других областях барьера Шоттки.

Связь электрического поля и потенциала для любых материалов с пространственно распределенным объемным зарядом описывается уравнением Пуассона. В одномерном приближении это уравнение имеет вид:

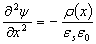   (2.30)

где ψ(x) - зависимость потенциала от координаты, ρ(x) - плотность объемного заряда, ε_s - диэлектрическая проницаемость полупроводника, ε₀ - диэлектрическая постоянная.

Заряд в области пространственного заряда барьера Шоттки для полупроводника n-типа обусловлен зарядом ионизованных доноров с плотностью N_D⁺. Поэтому

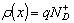   (2.31)

При интегрировании уравнения Пуассона учтем, что величина электрического поля E(x) = -∇φ

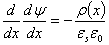   (2.32)

или

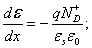   (2.33)

Проведем интегрирование уравнения (2.33). Выберем константу интегрирования из расчета, что при x = W электрическое поле Е равно нулю.

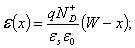   (2.34)

Из соотношения (2.34) следует, что электрическое поле Е максимально на границе металл-полупроводник (x = 0), линейно спадает по области пространственного заряда и равно нулю на границе ОПЗ - квазинейтральный объем полупроводника (x = W).

Для нахождения распределения потенциала (а следовательно и зависимости потенциальной энергии от координаты) проинтегрируем еще раз уравнение (2.34) при следующих граничных условиях: x = W, ψ(W) = 0. Получаем

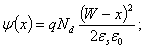   (2.35)

Максимальное значение потенциала реализуется при x=0 и составляет значение

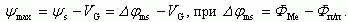   (2.36)

В этом случае можно рассчитать значение ширины обедненной области W, подставляя соотношение (2.36) в (2.35):

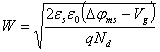   (2.37)

Соотношение (2.37) является очень важным уравнением для барьерных структур. В дальнейшем будет показано, что это уравнение является универсальным и описывает зависимость ширины обедненной области W от приложенного напряжения V_G и легирующей концентрации N_D для большинства барьерных структур. На рисунке 2.6 приведена диаграмма, иллюстрирующая распреде-ление электрического поля и потенциала в барьере Шоттки при обратном смещении, рассчитанных на основании соотношений (2.34) и (2.35).

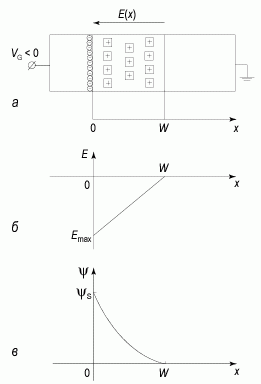
Рис. 2.6. Диаграмма, иллюстрирующая распределение электрического поля и потенциала в барьере Шоттки:
а) структура барьера Шоттки при обратном смещении;
б) распределение электрического поля в ОПЗ;
в) распределение потенциала в ОПЗ