Полупроводниковые диоды - СтабилитроныТвердотельная электроника. Учебное пособие.
4.4. Стабилитроны
Стабилитроном называется полупроводниковый диод, вольт-амперная характеристика которого имеет область резкой зависимости тока от напряжения на обратном участке вольт-амперной характеристики.
ВАХ стабилитрона имеет вид, представленный на рисунке 4.9.
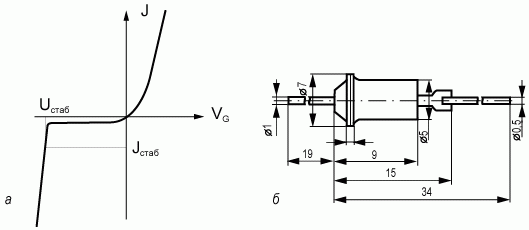
Рис. 4.9. Вольт-амперная характеристика (а) и конструкция корпуса (б) стабилитрона
При достижении напряжения на стабилитроне, называемого напряжением стабилизации Uстаб, ток через стабилитрон резко возрастает. Дифференциальное сопротивление Rдиф идеального стабилитрона на этом участке ВАХ стремится к 0, в реальных приборах величина Rдиф составляет значение: Rдиф ≈ 2÷50 Ом.
Основное назначение стабилитрона - стабилизация напряжения на нагрузке, при изменяющемся напряжении во внешней цепи. В связи с этим последовательно со стабилитроном включают нагрузочное сопротивление, демпфирующее изменение внешнего напряжения. Поэтому стабилитрон называют также опорным диодом.
Напряжение стабилизации Uстаб зависит от физического механизма, обуславливающего резкую зависимость тока от напряжения. Различают два физических механизма, ответственных за такую зависимость тока от напряжения, - лавинный и туннельный пробой p-n перехода.
Для стабилитронов с туннельным механизмом пробоя напряжение стабилизации Uстаб невелико и составляет величину менее 5 вольт: Uстаб < 5 В. Для стабилитронов с лавинным механизмом пробоя напряжение стабилизации обычно имеет большие значения и составляет величину более 8 вольт: Uстаб > 8 В.
Туннельный пробой в полупроводниках
Проанализируем более подробно механизмы туннельного и лавинного пробоя.
Рассмотрим зонную диаграмму диода с p-n переходом при обратном смещении при условии, что области эмиттера и базы диода легированы достаточно сильно (рис. 4.10).
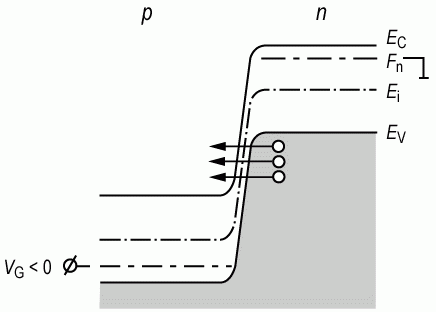
Рис. 4.10. Зонная диаграмма диода на базе сильнолегированного p-n перехода при обратном смещении
Квантово-механическое рассмотрение туннельных переходов для электронов показывает, что в том случае, когда геометрическая ширина потенциального барьера сравнима с дебройлевской длиной волны электрона, возможны туннельные переходы электронов между заполненными и свободными состояниями, отделенными потенциальным барьером.
Форма потенциального барьера обусловлена полем p-n перехода. На рисунке 4.11 схематически изображен волновой пакет при туннелировании через потенциальный барьер треугольной формы.
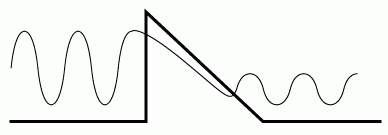
Рис. 4.11. Схематическое изображение туннелирования волнового пакета через потенциальный барьер
Возьмем уравнение Шредингера Hψ = Eψ, где H - гамильтониан для свободного электрона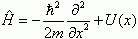 
, Е - энергия электрона.
Введем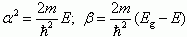 
Тогда снаружи от потенциального барьера уравнение Шредингера будет иметь вид:
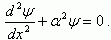
Внутри потенциального барьера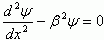 
.
Решение для волновых функций электрона будем искать в следующем виде:
Используем условие непрерывности для волновой функции и ее производные ψ, dψ/dx на границах потенциального барьера, а также предположение об узком и глубоком потенциальном барьере (βW >> 1).
В этом случае для вероятности туннельного перехода Т получаем:
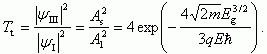
Выражение для туннельного тока электронов из зоны проводимости на свободные места в валентной зоне будет описываться следующим соотношением:
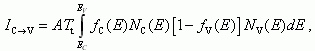
где использованы стандартные обозначения для функции распределения и плотности квантовых состояний.
При равновесных условиях на p+-n+ переходе токи слева и справа друг друга уравновешивают: IC→V = IV→C.
При подаче напряжения туннельные токи слева и справа друг друга уже не уравновешивают:
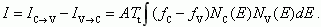(4.18)Здесь fC, fV - неравновесные функции распределения для электронов в зоне проводимости и валентной зоне.
Для барьера треугольной формы получено аналитическое выражение для зависимости туннельного тока Jтун от напряженности электрического поля Е следующего вида:
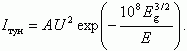(4.19)За напряженность электрического поля пробоя Eпр условно принимают такое значение поля Е, когда происходит десятикратное возрастание обратного тока стабилитрона: Iтун = 10·I0.
При этом для p-n переходов из различных полупроводников величина электрического поля пробоя Eпр составляет значения: кремний Si: Eпр = 4·105 В/см; германий Ge: Eпр = 2·105 В/см. Туннельный пробой в полупроводниках называют также зинеровским пробоем.
Оценим напряжение Uz, при котором происходит туннельный пробой. Будем считать, что величина поля пробоя Eпр определяется средним значением электрического поля в p-n переходе Eпр = Uобр/W . Поскольку ширина области пространственного заряда W зависит от напряжения по закону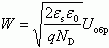 
, то, приравнивая значения W из выражений 
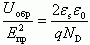, получаем, что напряжение туннельного пробоя будет определяться следующим соотношением [5, 2]:
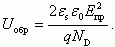(4.20)Рассмотрим, как зависит напряжение туннельного пробоя от удельного сопротивления базы стабилитрона. Поскольку легирующая концентрация в базе ND связана с удельным сопротивлением ρбазы соотношением ND = 1/ρμe, получаем:
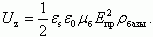(4.21)Из уравнения (4.21) следует, что напряжение туннельного пробоя Uz возрастает с ростом сопротивления базы ρбазы.
Эмпирические зависимости напряжения туннельного пробоя Uz для различных полупроводников имеют следующий вид:
германий (Ge): Uz = 100ρn + 50ρp;
кремний (Si): Uz = 40ρn + 8ρp,
где n, p - удельные сопротивления n- и p-слоев, выраженные в (Ом·см).
Лавинный пробой в полупроводниках
Рассмотрим случай однородного электрического поля в полупроводнике. Если двигаясь вдоль силовых линий электрического поля электрон на расстоянии, равном длине свободного пробега λ, наберет энергию, равную либо большую, чем ширина запрещенной зоны, то, неупруго рассеиваясь, этот электрон может вызвать генерацию еще одной электронно дырочной пары. Дополнительно нагенерированные свободные носители также будут участвовать в аналогичном процессе. Это явление лавинного размножения свободных носителей в условиях сильного электрического поля получило название лавинного пробоя. На рисунке 4.12 показана схема, иллюстрирующая лавинный пробой.
Размеры геометрической области полупроводника W, в которой происходит лавинное умножение, должны быть существенно больше длины свободного пробега электрона λ. Соотношения, определяющие условие лавинного пробоя, будут следующие:
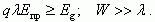(4.22)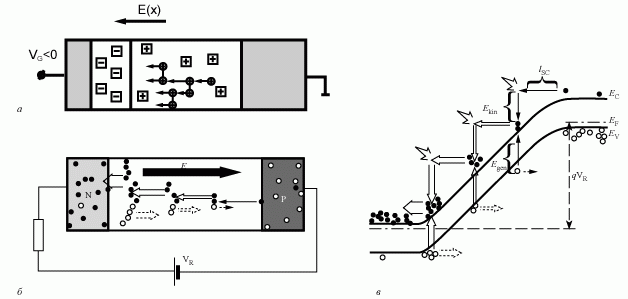
Рис. 4.12. Схема, иллюстрирующая лавинный пробой в однородном полупроводнике [27, 10]:
а) распределение электрического поля, доноров и акцепторов и свободных носителей; б) распределение токов; в) зонная диаграмма, иллюстрирующая лавинное умножение в ОПЗ
Одним из параметров лавинного пробоя является коэффициент лавинного умножения M, определяемый как количество актов лавинного умножения в области сильного электрического поля. Если обозначить начальный ток I0, то после лавинного умножения величина тока будет иметь вид: I = M·I0,
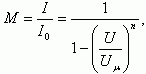
где Uμ - напряжение лавинного пробоя, U - напряжение, n - коэффициент, равный 3 или 5 для Ge или Si соответственно.
Для несимметричного p+-n перехода расчет дает следующее значение напряжения лавинного пробоя VB при условии, что максимальное значение поля в ОПЗ p+-n перехода можно приближенно оценить как среднее:
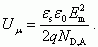(4.23)Величина электрического поля Еm, определяемая соотношением (4.23), зависит от величины и типа легирующей концентрации ND, NA, температуры и лежит в диапазоне Еm = (4÷5)·105 В/см для кремния и Еm = (2÷3)·105 В/см для германия.
Приборные характеристики стабилитронов
Основными характеристиками стабилитрона являются ток Iст и напряжение Uст стабилизации, дифференциальное напряжение стабилитрона rст и температурная зависимость этих параметров. На рисунке 4.13 приведены дифференциальные параметры различных стабилитронов.
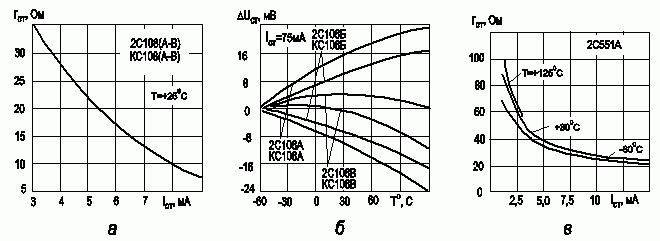
Рис. 4.13. Дифференциальные параметры различных стабилитронов:
а) зависимость дифференциального сопротивления от прямого тока 2С108; б) зависимость изменения напряжения стабилизации от температуры для различных типономиналов стабилитрона 2С108; в) зависимость дифференциального сопротивления от прямого тока 2С351
Как следует из приведенных данных, значение дифференциального сопротивления для стабилитронов обратно пропорционально току стабилизации и составляет десятки Ом при рабочих параметрах токов. Точность значения напряжения стабилизации составляет десятки милливольт в стандартном температурном диапазоне.
Copyright © 2003-2008 Авторы
| Ваш комментарий к статье | ||||
