Биполярные транзисторы - Частотные и импульсные свойства транзисторовТвердотельная электроника. Учебное пособие.
5.18. Частотные и импульсные свойства транзисторов
Процесс распространения инжектированных в базу неосновных носителей заряда от эмиттерного до коллекторного перехода идет диффузионным путем. Этот процесс достаточно медленный и инжектированные из эмиттера носители достигнут коллектора не ранее, чем за время диффузии носителей через базу, определяемое как τD = v/W ~ W²/D. Такое запаздывание приведет к сдвигу фаз между током в эмиттерной и коллекторной цепи. Рассмотрим эти процессы более подробно для биполярного транзистора в схеме с общей базой.
Предположим, что в эмиттерной цепи от генератора тока в момент времени t = 0 подали импульс тока длительностью Т большей, чем характеристическое время диффузии τD. Ток в коллекторной цепи появится только через время τD причем вследствие распределения по скоростям в процессе диффузионного переноса фронт импульса будет размываться в пределах временного интервала t1. Через время τD + t1 в коллекторной цепи установится ток, равный α0Iэ. Через время t = T, когда импульс тока в эмиттерной цепи закончится, в коллекторной цепи будет продолжать течь ток α0Iэ до времени T + D. Затем также вследствие размытия фронта импульса коллекторный ток будет спадать до нуля за время t1, после T + τD. На рисунке 4.24 показаны эпюры эмиттерного (пунктир) и коллекторного (сплошная линия) токов при трансляции эпюра коллекторного тока на интервал времени τD.
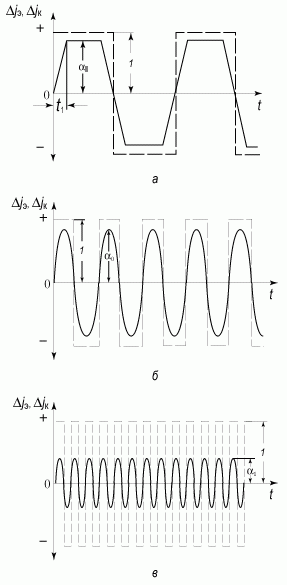
Рис. 5.26. Эпюры эмиттерного (пунктир) и коллекторного (сплошная линия) токов при трансляции эпюра коллекторного тока на интервал времени τD [28, 15]:
а) длительность импульса тока в эмиттерной цепи больше, чем время диффузии неравновесных носителей через базу; б) длительность импульса тока сравнима со временем диффузии; в) длительность импульса тока меньше, чем время диффузии
Таким образом, при больших длительностях импульсов эмиттерного тока частота сигналов в коллекторной цепи останется неизменной, амплитуда коллекторного тока составит Iк = αIэ, и будет наблюдаться сдвиг фаз φ между эмиттерным Iэ и коллекторным Iк токами. Величина тангенса φ будет равна:
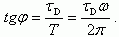(5.44)Из уравнения (5.44) следует, что в общем случае величина сдвига фаз между эмиттерным и коллекторным токами будет определяться как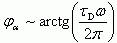 
.
Сдвинем для удобства Δjк и Δjэ на величину τD по временной оси, тем самым совместим их. Будем наращивать частоту переменного сигнала или уменьшать период эмиттерного тока.
При длительности эмиттерного импульса T/4 > τD "плоского" участка на коллекторном токе Iк = Iэ уже не будет (рис. 5.26б). При дальнейшем уменьшении периода эмиттерного импульса Т начнет уменьшаться амплитудное значение коллекторного тока, поскольку за это время инжектированные носители не успевают дойти до коллекторного перехода (рис. 5.26в). На языке коэффициента передачи это соответствует возникновению частотной зависимости амплитудного значения коэффициента передачи α(ω).
Таким образом, величина α(ω) характеризует коэффициент передачи тока в схеме с общей базой и определяется модулем |α| и фазой φα, причем зависимость α(ω) возникает вследствие инерционности переноса носителей от эмиттера к коллектору. На рисунке 5.27 показаны эпюры эмиттерного и коллекторного токов для этого случая.
Частота входного сигнала ω, при которой модуль коэффициента передачи |α| уменьшается в 21/2 раз по сравнению со статическим значением α0, называется предельной частотой усиления по току ωα биполярного транзистора в схеме с общей базой:
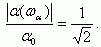(5.45)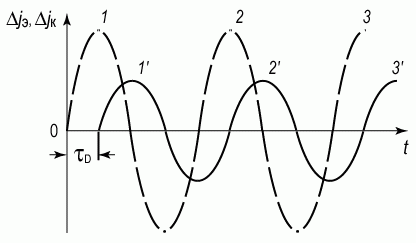
Рис. 5.27. Эпюры эмиттерного (пунктирная линия) и коллекторного (сплошная линия) токов биполярного транзистора в схеме с общей базой для случая T/4 < τD
Поскольку коэффициент передачи α определяется произведением коэффициентов инжекции γ и переноса κ, то основное значение в зависимости α(ω) играет зависимость коэффициента переноса от частоты κ(ω).
Для определения частотной зависимости коэффициента переноса κ(ω) нужно решить уравнение непрерывности при наличии постоянных и переменных составляющих в эмиттерном токе и напряжении:
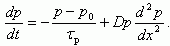(5.46)Считаем, что
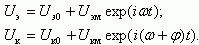(5.47)У эмиттерного и коллекторного переходов при приложении переменного напряжения протекают переменные токи iэ и iк. Очевидно, что из-за наличия в выражении (5.47) множителя exp(iωt) в решении (5.46) появятся временные зависимости концентрации неосновных носителей p(x,t), а соответственно и в токах также появятся временные зависимости. Решение уравнения непрерывности дает следующее выражение для комплексной величины коэффициента переноса:
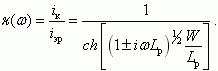(5.48)При ω = 0 (статические характеристики) из соотношения (5.48) следует выражение для статического коэффициента передачи κ (ω = 0):
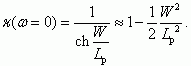(5.49)Найдем из соотношения (5.48) значение граничной частоты ωα = ωκ, при которой модуль величины κ(ω) уменьшится в 21/2 раз:
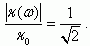
Преобразуем соотношение (5.48) в более удобный вид, считая, что значение в круглых скобках под знаком гиперболического косинуса меньше единицы. Тогда
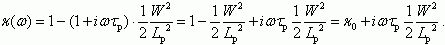(5.50)Для модуля коэффициента переноса
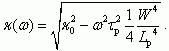
Согласно определению граничной частоты ωα получаем:
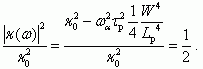
Следовательно,
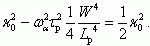Учтем, что κ0 ~ 1. Тогда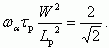 
Используя соотношение Lp2 = Dpτp, получаем:
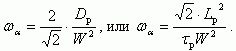(5.51)Более точное решение уравнения непрерывности дает следующее выражение для предельной частоты усиления по току ωα:
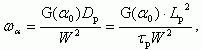(5.52)где G(α0) ≈ 2,53.
С учетом выражения для граничной частоты ωα (5.52) соотношение для комплексного значения коэффициента переноса κ (5.50) преобразуется к следующему виду:
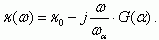(5.53)Графическая зависимость модуля коэффициента переноса κ и угла фазового сдвига φ от частоты входного сигнала приведена на рисунке 5.28.
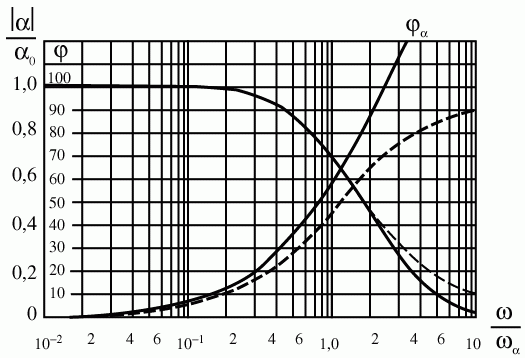
Рис. 5.28. Зависимость модуля коэффициента переноса |κ(ω)| и угла фазового сдвига φα от частоты входного сигнала ω [28, 15]
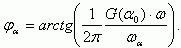
При значении частоты входного сигнала ω, равной граничной частоте ωα (ω/ωα = 1,0), значение модуля коэффициента переноса будет составлять |κ(ω)| = 0,71, а величина фазового сдвига между эмиттерным и коллекторным током будет равна φα = 600.
Из общих соображений следует, что когда ω-1 ~ τD, величина сдвига фаз составит φ = 550, но величина модуля коэффициента передачи |κ(ω)| при этом еще не изменится.
Для представления в эквивалентных схемах амплитудной и фазочастотной зависимостей α(ω) используют RС-цепочку (рис. 5.29). В такой цепочке если входной переменный сигнал α0Iэ, то ток в цепи резистора R будет отображать амплитудную и фазочастотную зависимости α(ω)Iэ.
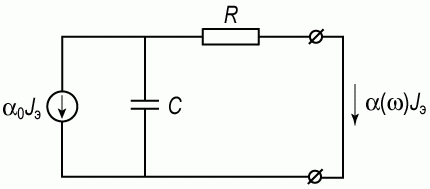
Рис. 5.29. RC-цепочка, иллюстрирующая амплитудную и фазочастотную зависимости α(ω)
По правилам сложения комплексных величин для модуля комплексного сопротивления Z для RC-цепочки получаем:
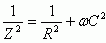, следовательно,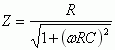 
Полный ток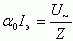 
.
Ток в цепи резистора IR будет равен:
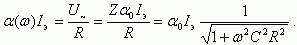
Следовательно,
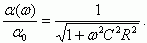(5.54)Поскольку для граничной частоты ωα справедливо соотношение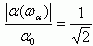 
, то из уравнения (5.55) следует, что ωα = 1/RC. С учетом сказанного получаем:
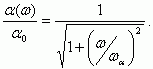(5.55)Для RС-цепочки сдвиг фаз φ между входным током α0Iэ и током в цепи резистора IR рассчитаем следующим образом. Сосчитаем сначала значение тока IC в цепи емкости C.
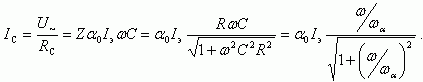
Тогда тангенс угла φ, как следует из векторной диаграммы токов RC-цепочки, будет равен:
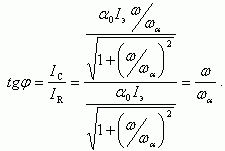(5.56)Изобразим в комплексной форме зависимости α(ω) для RC-цепочки в следующем виде:
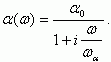(5.57)Из уравнения (5.57) следует, что в этом случае модуль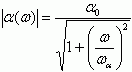 
, фазовый сдвиг tg(φα) = ω/ωα, что полностью соответствует соотношениям (5.56) и (5.55).
Из соотношения (5.56) следует, что сдвиг фаз φ для RC-цепочки при ω = ωα составляет значение φ = 550. Поэтому к RС-цепочке для более адекватного отображения реальной зависимости α(ω) нужно добавить еще генератор тока с дополнительным фазовым сдвигом, не меняющий амплитуды тока,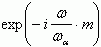 
.
При величине коэффициента m = 0,2 фазовый сдвиг при частоте ω = ωα будет составлять величину Δφ = 600.
Тогда
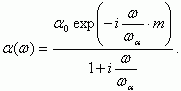(5.58)Рассмотрим амплитудную и фазочастотную зависимости коэффициента передачи базового тока для биполярного транзистора в схеме с общим эмиттером. Коэффициент передачи эмиттерного тока α и коэффициент передачи базового тока β связаны стандартным соотношением:
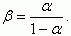
Для нахождения связей частотных параметров биполярного транзистора в схеме с общей базой и в схеме с общим эмиттером рассмотрим векторные диаграммы для токов, приведенные на рисунке 5.30.
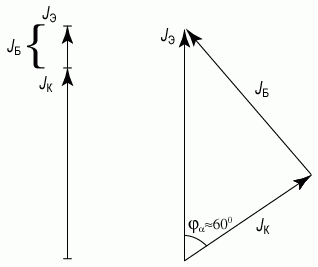
Рис. 5.30. Векторная диаграмма токов для биполярного транзистора в схеме с общей базой, иллюстрирующая фазовый сдвиг между эмиттерным и коллекторным током
При малой частоте ω << ωα фазы эмиттерного Iэ, коллекторного Iк и базового Iб токов, как видно из рисунка 5.30а, совпадают и величина базового тока Iб равна разности Iэ - Iк.
При значении частоты эмиттерного тока, равной граничной частоте ω = ωα, в схеме с общей базой коллекторный ток в 21/2 раз меньше эмиттерного тока. На векторной диаграмме (рис. 5.30б) видно, что при фазовом сдвиге = 600 величина базового тока Iб также равна разности Iэ - Iк, но в этом случае речь идет о векторной разности. Модуль же значения базового тока Iб при ω = ωα значительно больше, чем при ω = 0. При этом видно, что величина коэффициента передачи базового тока β = Iк/Iб при ω = 0 значительно больше, чем при ω = ωα. Если модуль коэффициента передачи эмиттерного тока α(ω) уменьшился при этом в 21/2 раз, то модуль коэффициента усиления базового тока β(ω) уменьшился существенно больше.
Определим предельную частоту ω усиления по току биполярного транзистора в схеме с общим эмиттером как частоту ωβ, при которой модуль коэффициента усиления β(ωβ) уменьшается в 21/2 раз по сравнению со статическим значением β0.
Найдем соотношение между предельной частотой для схемы с общим эмиттером ωβ = β(ω)/β0 = 1/(21/2) и предельной частотой для схемы с общей базой ωα = α(ω)/α0 = 1/(21/2). Для этого проанализируем векторную диаграмму для токов при условии, что ω = ωβ. В этом случае величина базового тока увеличилась в 21/2 раз. Из векторной диаграммы (рис. 5.31) видно, что фазовый сдвиг φ между эмиттерным и коллекторным током будет незначителен.
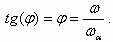
Поскольку в рассматриваемом случае ω = ωβ, то φ = ωβ/ωα.
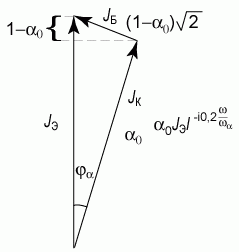
Рис. 5.31. Векторная диаграмма токов в биполярном транзисторе в схеме с общим эмиттером для случая ω = ωβ
При малых φ и при α0 → 1 (см. рис. 5.31) следует, что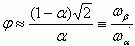 
. Более точный расчет дает следующее выражение:
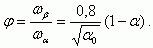
С учетом этого получаем:
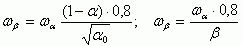или оценочное отношение ωα/ωβ ~ β.
Таким образом, в схеме с общим эмиттером предельная частота усиления по току ωβ много меньше, чем предельная частота ωα в схеме с общей базой.
Частоты ωα и ωβ могут быть выражены через физические параметры транзистора:
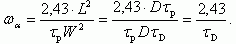(5.59)Величина ωβ ≈ ωα/β, а значение β равно β = (1/2)(L/W)2, тогда
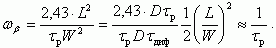(5.60)Для описания частотной зависимости β(ω) подставим в выражение для β частотно-зависимый коэффициент переноса α(ω). Получим:
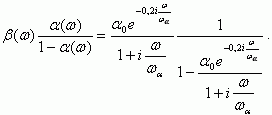
В заключение раздела построим эквивалентную схему биполярного транзистора на высоких частотах для схемы с общей базой (рис. 5.32).
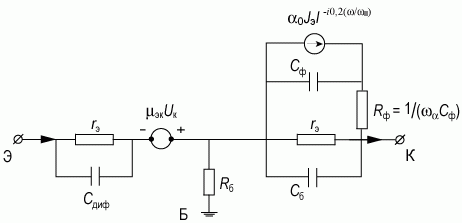
Рис. 5.32. Эквивалентная схема биполярного транзистора на высоких частотах для схемы с общей базой
На приведенной эквивалентной схеме основные параметры элементов в эмиттерной, базовой и коллекторной цепи такие же, как и для эквивалентной схемы при малых частотах. Различие этих двух схем проявляется в коллекторной цепи, где частотная зависимость коэффициента передачи α(ω) изображена в виде фазосдвигающей RC-цепочки Сф и Rф в коллекторной цепи.
Copyright © 2003-2008 Авторы
| Ваш комментарий к статье | ||||
